Warlic
- 32
- 0
I have spent quite some time trying to get this, can someone please help me understand this?
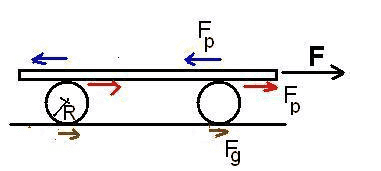
A plank is being pulled by a constant force F, it rests on top of two identitcal sylinders - there is rolling without slipping. What I don't understand is, why does F(p) - red arrow force, affect the acceleration of the center of mass of the cylinder. Isnt the only thing the red arrow F(p) does, to make it rotate - so it only affects its angular acceleration, and not the acceleration of center of mass of cylinders - while F(g) is the only force that affects the acceleration of center of mass.?
And a second question:
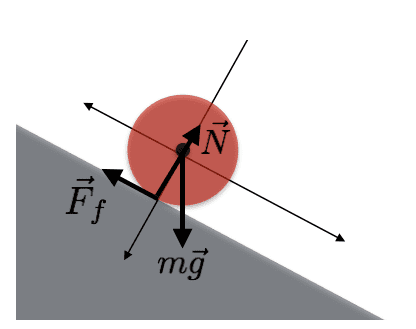
Disk rolls down an incline, here there is also rolling without slipping. But why in the world is the friction force pointing upwards. The disk is rolling clockwise ,shouldn't the friction force be pointing downwards - opposite of what's in the figure? Because on the first picture the cylinder is also rolling clockwise, and the friction force is acting along the same direction as the cylinder is moving - to the right.
A plank is being pulled by a constant force F, it rests on top of two identitcal sylinders - there is rolling without slipping. What I don't understand is, why does F(p) - red arrow force, affect the acceleration of the center of mass of the cylinder. Isnt the only thing the red arrow F(p) does, to make it rotate - so it only affects its angular acceleration, and not the acceleration of center of mass of cylinders - while F(g) is the only force that affects the acceleration of center of mass.?
And a second question:
Disk rolls down an incline, here there is also rolling without slipping. But why in the world is the friction force pointing upwards. The disk is rolling clockwise ,shouldn't the friction force be pointing downwards - opposite of what's in the figure? Because on the first picture the cylinder is also rolling clockwise, and the friction force is acting along the same direction as the cylinder is moving - to the right.