Libohove90
- 40
- 0
Homework Statement
I figured I'll try this again.
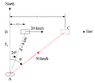
A battleship steams due east at 24 km/h. A submarine 4.0 km away fires a torpedo that has a speed of 50 km/h. If the ship is seen 20º east of north, in what direction should the torpedo be fired to hit the ship?
Homework Equations
Battleships motion: x = x_{}0 + v_{}xt
Torpedo's motion: x' = v cos \phi t
y' = y_{}0' + v sin \phi t
The Attempt at a Solution
In my earlier thread, someone suggested that this is a related rate problem. I am not sure how to do that.
I tried vector addition, but two are velocity vectors (ship and torpedo's velocity) and one is a position vector (the distance between them). This does not seem like a difficult problem, but I need some guidance real bad here, it's halting my progress to doing other problems because I am too stubborn. I appreciate any useful help...thank you