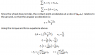Rolling Wheel Paradox: Is it True or a Model Problem?

[e-o]

Hi,

I'm trying to model a wheel that is placed on top of a moving platform.
The problem is that I'm running into a situation that seems very counter intuitive. I'm not sure if its a problem with my model or not. I've attached a picture that demonstrates the problem.

To begin, neither the wheel nor the platform is moving. At some time (say t = 0), the platform begins accelerating in one direction (lets say its to the left) at a constant acceleration. For simplicity, I'm just assuming the mass of the platform is infinite (so that the wheel doesn't affect the motion of the platform).

So the wheel starts to accelerate with the platform, but also rolls in a direction that opposes the movement of the platform (assume it never slips). I've attached my derivation of the force and torque acting on the wheel as the platform moves.

Now the problem comes in when I look at how many rotations the wheel makes. If the radius of the wheel is R and the length of the platform is 2πR (the circumference of the wheel), then I would expect the wheel to make exactly one full rotation before falling off the platform. Instead I find that it depends on the moment of inertia of the wheel, for example, a disk makes 2 rotations.

Can someone explain if this is true, or just a problem with my derivation?

 

[NobodySpecial]

Intuitively I would have though it should depend on the intertia.
A very light wheel will tend to move with the platform - not rotating much, while a heavy wheel will tend to stay in the same place (relative to an outside point) and so rotate more

 

[AlephZero]

Common sense says this is obviously wrong, and the wheel takes one revolution to cross the platform!

So the real question is where your derivation went wrong. I think that is on the second page. If the acceleration of the wheel is a_w, its angular acceleration is a_w/R relative to the platform. But the platform in not an inertial reference frame because it is accelerating!

If you want to work relative to the platform, you have to include the fictitious d'Alembert force -m_w a_p acting on the wheel. Everything should then work out as properly.

The other way is to work in an inertial reference frame attached to the ground. In that case the rotational accleration of the wheel is a_w/R, but its translational accleration is a_w + a_p not a_w.

 

[AlephZero]

Intuitively I would have though it should depend on the intertia.
A very light wheel will tend to move with the platform - not rotating much, while a heavy wheel will tend to stay in the same place (relative to an outside point) and so rotate more

The time it takes for the wheel to travel across the platform depends on its inertia. If the inertia is low relative to the mass the wheel rotates more easily and the translational acceleration is small . If the inertia is high the wheel will rotate slower and have a higher translational accleration (relative to the ground) so it will take longer to roll across the platform.

But if the platform is the same length as the circumference of the wheel and the wheel doesn't slip, it takes one rev to cross the platform just from the kinematics of the situation. The dynamics of the problem are irrelevant, so long as the wheel doesn't slip.

 

[e-o]

Aha! Yes thank you.

It seems obvious now that you point it out, but I've been scratching my head all day trying to figure this out. So again, thank you!

 

[rcgldr]

a disk makes 2 rotations.

The moment of inertia has an effect. A hollow cylinder with angular inertia of m R² would never move linearly. It's surface speed would accelerate at the same speed as the platform, but there would be no linear acceleration. Your formula for time would end up dividing by zero.

 

[e-o]

That's a good point. It's an elegant way to check that my formulas weren't correct, I wish I had thought of that earlier!

For my own (and anyone elses) future reference, I've updated the derivation and attached it to this post. It's slightly different from AlephZero's suggested solution (the terms are just defined differently), but as far as I can tell, its equivalent. Hopefully everything is correct this time.

The formula for the time taken for the wheel to reach the end of the platform confirms that higher moments of inertia result in longer travel times.

 

[rcgldr]

The moment of inertia has an effect. A hollow cylinder with angular inertia of m R² would never move linearly.

I meant to state using your formula a hollow cylinder ... would never move linearly.

Note in your formulas, if distance to the right is positive, then accelerations to the left are negative.

With respect to the ground, a_w = ( I_w / (1 + I_w)) a_p
With respect to the platform, a_w - a_p = (-1 / (1 + I_w)) a_p

With respect to the ground, for a solid uniform cylinder, a_w = 1/3 a_p
With respect to the platfom, for a solid uniform cylinder, a_w - a_p = -2/3 a_p

With respect to the ground, for a hollow cylinder, a_w = 1/2 a_p
With respect to the platfom, for a solid uniform cylinder, a_w - a_p = -1/2 a_p

 

[e-o]

I meant to state using your formula a hollow cylinder ... would never move linearly.

Yes, I assumed that's what you meant.

Note in your formulas, if distance to the right is positive, then accelerations to the left are negative.

I was a bit sloppy keeping track of the signs, but I believe this is correct (although my mind's in a bit of a knot thinking about it now...).
The distance formula I wrote is for the distance the wheel travels relative to the platform. So if the platform acceleration is to the left, then the wheel will travel to the right (relative to the platform at least). But ya, the absolute distance traveled by the wheel should be to the left.

 

[rcgldr]

I was a bit sloppy keeping track of the signs.

In the bottom formula for t, the right most radical should have a negative sign in the expression (note ap is negative):

t = sqrt( - (1 + (I_w / (m R²))) (4 pi R) / a_p )

I cleaned up my previous post to show some examples.

 

[e-o]

Oh yes, true, thank you.

I had assumed that the accelerations were in the positive direction, which means I should have been solving for the case where d = -2πR, that should account for the missing minus sign in the expression for t. It would also change the sign of the angle to +2π, which seems to make more sense as well.

Incidentally, I've tried this 'experiment' out in real life (well, just sliding a platform with a wheel on top). For whatever reason, if the platform moves slowly enough, the wheel never rotates. Any idea what would stop it from rolling? I figure it might have something to do with the same effect that causes rolling resistance, or possibly the wheel just isn't balanced properly. Mind you I did this with a toy wheel and a scrap piece of paper on my desk haha, so there's a lot of uncontrolled variables at work I guess.