Rotating rod with weight

[huskydc]

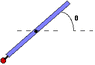
A uniform rod is pivoted at its center and a small weight of mass M = 5.29 kg is rigidly attached to one end. You may neglect the size of the weight and assume it is located right at the end of the rod.

Suppose that the rod has length L = 6.8 m and mass mrod = 10.6 kg. Suppose also that there are no external forces applied (i.e. Fh = Fv = 0). The system is released from rest at the q = 37° angle. What is the angular acceleration just after it is released?


i did the following;

net torque = I * alpha

find I of the rod+weight system. and net toque, and solve for alpha

but i have a question regarding the force of the rod itself...
i've been told to treat the rod as if all its mass were concentrated at its center of mass. but is that with or without the weight attached to it?

i mean, w/o the weight, the center of mass of the rod is at the axis point., thus no torque on that point.

 

[Doc Al]

Suppose that the rod has length L = 6.8 m and mass mrod = 10.6 kg. Suppose also that there are no external forces applied (i.e. Fh = Fv = 0). The system is released from rest at the q = 37° angle. What is the angular acceleration just after it is released?

I assume you mean no forces except that provided by the pivot.

i did the following;

net torque = I * alpha

find I of the rod+weight system. and net toque, and solve for alpha

OK. Be sure you calculate the total rotational inertia of the "mass + rod".

but i have a question regarding the force of the rod itself...
i've been told to treat the rod as if all its mass were concentrated at its center of mass. but is that with or without the weight attached to it?

For the purpose of caculating the torque produced by the weight of the rod, assume that gravity acts at the center of the uniform rod. But that's for the rod only, not for the extra mass at the end. The weight of that added mass acts right at the end.

i mean, w/o the weight, the center of mass of the rod is at the axis point., thus no torque on that point.

Exactly.

 

[mezarashi]

i've been told to treat the rod as if all its mass were concentrated at its center of mass. but is that with or without the weight attached to it?

i mean, w/o the weight, the center of mass of the rod is at the axis point., thus no torque on that point.

Would it be any consolation if I told you that I have no idea as well why you were asked to do that?

 

[Doc Al]

Would it be any consolation if I told you that I have no idea as well why you were asked to do that?

They were gently reminding you that the center of mass/gravity of a uniform rod is at its center. (Although one should know this.)

 

[huskydc]

so would the net torque be just of the torque exerted by mass?

 

[Doc Al]

That is correct.

 

[huskydc]

i'm getting myself more confused than ever, the net torque is just of the torque exerted by mass itself. the moment of inertia for rod is (1/12) M L^2. the rod's concentrated mass is still at the axis. so:

total moment of inertia: (1/12) (5.29)(6.8^2) -- mass

do i add (1/12) (10.6)(6.8^2)? if the rod's mass is at the center, does it have moment of inertia...? i guess that's my question

 

[Doc Al]

Both the rod and the mass contribute to the moment of inertia of the "rod + mass" system. Add their contributions together to get the total moment of inertia.

The rod's mass is not just at the center! (But the force of gravity acts at the center.) As an extended body, the rod has a moment of inertia given by your formula.

The moment of inertia of a point mass M a distance R from the axis is simply $M R^2$.

 

[huskydc]

ok, here's my take on total of moment of inertia:

1/12) (5.29)(6.8^2) + (10.6)(3.4^2) ?

and torque of mass:

3.4 * (5.29 * 9.81) sin37 ??

i'm sorry, I'm a microbiology major, I'm really really bad at physics... i really thought i had the right answer, i mean I've figured out the other parts to this problem, just not this one...

 

[Doc Al]

ok, here's my take on total of moment of inertia:

1/12) (5.29)(6.8^2) + (10.6)(3.4^2) ?

I think you have the masses interchanged.

and torque of mass:

3.4 * (5.29 * 9.81) sin37 ??

Looks OK if the angle is measured from vertical.

 

[huskydc]

so...

I alpha = Torque

(1/12) (10.6)(6.8^2) + (5.29)(3.4^2) alpha = 3.4 * (5.29 * 9.81) sin37

solve for alpha?


(well i already did, b/c I'm getting a little desperate..and its wrong)

 

[Doc Al]

The angle is measured from the horizontal (see my last post), so use cosine instead of sine.

 

[wrkinhard]

I have a question that piggy backs that problem...what would the angular velocity be whent he rod is vertical?

I know that mgh=1/2Iw^2..but how do I get the potential energy of the rod?

 

[Doc Al]

Since the rod's center doesn't move, its potential energy doesn't change.