Mateus Buarque
- 6
- 0
The figure below shows a system in equillibrium. The pulley and the springs (both with constants "k") are ideal. The period of oscillation of the mass A is given by:
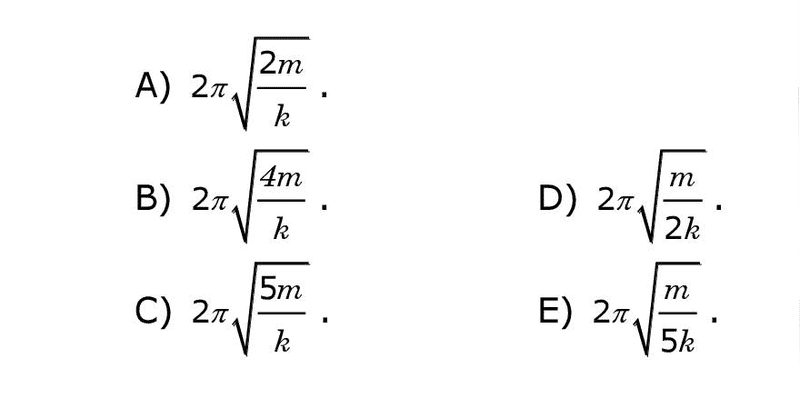
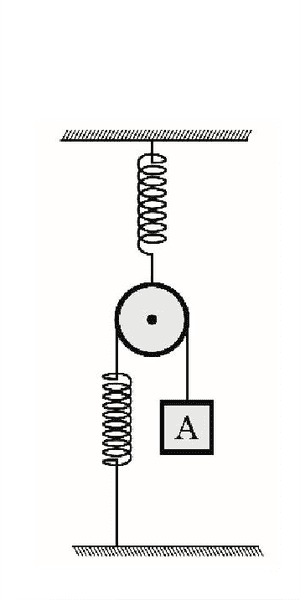




Relevant equations:
F = -kx (SHM)
I tried to do a "force diagram" and set up some geometric relations but it´s not working.




Relevant equations:
F = -kx (SHM)
I tried to do a "force diagram" and set up some geometric relations but it´s not working.
 !
!