SebastianRM
- 39
- 4
- Homework Statement
- A) Analyze velocity profile
B) Determine shear stress at both walls
- Relevant Equations
- Fluid flow between two parallel plates with slip of,
$$ \delta u \approx l (du/dy)$$
The problem states:
Two parallel plates separated by distance h, the plate at the top moves with velocity V, while the one at the bottom remains stationary.
My initial approach was:
I considered, ##du/dy = V/h## and for the shear stress ##\tau = \mu \frac{\partial u}{\partial y}##
For $$\frac{\partial u}{\partial y} = \frac{U_{top}-U_{bottom}}{h}$$
Where I considered the fluid's velocity at the top plate to be, ##U_{top} = V - \delta u## , and at the bottom, ##U_{bot} = 0 + \delta u##.
In order to improve my understanding, I searched for a diagram that illustrated the phenomena, which shows (apologies for the low quality) :
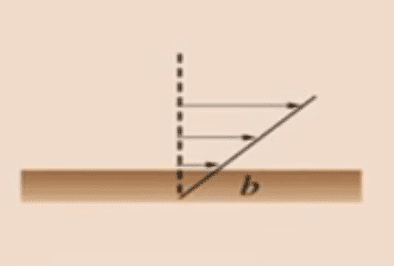
This ##b## distance in the diagram is the ##l## of my equation at the top. So I am wondering if it should be included as part of the ##dy## term, as ##dy = h - l## or should it be part of the ##\partial y = h - l ## or if my original analysis was correct?
Thanks a lot guys, your time and help are very appreciated.
Two parallel plates separated by distance h, the plate at the top moves with velocity V, while the one at the bottom remains stationary.
My initial approach was:
I considered, ##du/dy = V/h## and for the shear stress ##\tau = \mu \frac{\partial u}{\partial y}##
For $$\frac{\partial u}{\partial y} = \frac{U_{top}-U_{bottom}}{h}$$
Where I considered the fluid's velocity at the top plate to be, ##U_{top} = V - \delta u## , and at the bottom, ##U_{bot} = 0 + \delta u##.
In order to improve my understanding, I searched for a diagram that illustrated the phenomena, which shows (apologies for the low quality) :
This ##b## distance in the diagram is the ##l## of my equation at the top. So I am wondering if it should be included as part of the ##dy## term, as ##dy = h - l## or should it be part of the ##\partial y = h - l ## or if my original analysis was correct?
Thanks a lot guys, your time and help are very appreciated.