boz27 said:
Let’s make it easier if you like
cos(θ1).exp(iθ2)
where θ1 and θ2 are constants in rad.
As you recommended I found in the following expression
[Exp(i(θ1+ θ2)) + Exp(i(θ2- θ1))] /2
İf I try to turn back to the cosine form I can not provide something like
cos(θ1+ θ2) or cos(θ1- θ2) or cos(θ1- θ2+ PI/2)...
OR
sin(θ1+ θ2) or sin(θ1- θ2) or sin(θ1- θ2+ PI/2)...
Sorry for the late reply, but I've been giving this thread some thought.
The best I can surmise, is that you might be incorrectly mixing terms in the time domain and the frequency domain. Terms such as cos(w_0 t) typically are found in the time domain. Terms like e^{j \theta} are typically found in the frequency domain.
Unfortunately, I didn't realize that until after I replied, and I think I might have just made the confusion worse. Sorry about that. Let me start over.
Suppose you have a time domain signal,
v_s(t) = Acos(\omega_0 t)
Call its frequency domain representation V(\omega _0). And suppose that in the frequency domain (sometimes called phasor representation), you determined the frequency response of some other signal to be V_c(\omega)/V_s(\omega) = H(\omega) = e^{j \theta}. In other words, suppose that you have determined that
V_c(\omega) = V_s e^{j \theta}.
When converting this to the time domain, the result is simply,
v_c(t) = Acos(\omega_0 t + \theta),
when working with sinusoidal steady-state analysis. That's what I meant by
trivial in my last post.

In general, when performing sinusoidal steady-state analysis (ignoring transients like when you close a switch or something), if you have
Y(\omega) = X(\omega)H(\omega)
then
|Y| = |X||H|
and
\angle Y = \angle X + \angle H
This is from topic of electric physics .
You have a voltage source as cos(wt) or cos(θ1) w=2.PI.f t: time
I have a low pass filter that is described as
exp(iθ2) (say transfer fonction in sinusoidal continuous form)
which is to make θ2 rad (or degrees) shift in phase with respect to input signal say cos(wt)
What am I going to see on scope at output ?=How the output will be seen in time domain ?
I am interested in reel part of the output
If I use MATLAB with simulink I can see a output voltage wave form that is shifted by θ2 with respect to input signal. (Lets ignore change in amplitude)
With best regards
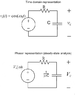
Perhaps this is a good time to show a concrete example. Suppose you have an AC voltage source connected to a series RC circuit, and you want to measure the voltage across the capacitor.
You can draw the circuit the normal way, but it makes it a little easier to draw the circuit in the phasor representation, since that makes it automatically ready for frequency domain analysis.
Finding the sinusoidal steady-state current is easy enough. We just divide the voltage by the total impedance,
I(\omega) = \frac{V_s}{R + \frac{1}{j \omega C}}
Multiply the current by the impedance of the capacitor to find the voltage we are looking for,
V_c(\omega) = \frac{V_s \frac{1}{j \omega C}}{R + \frac{1}{j \omega C}} = \frac{V_s \frac{1}{j \omega C}}{\frac{1+ j \omega RC}{j \omega C}} = \frac{V_s}{1 + j \omega RC}
The transfer function is then,
H(\omega) = \frac{V_c(\omega)}{V_s(\omega)} = \frac{1}{1+ j \omega RC}
The denominator is a complex number. It can be written in polar form.
H(\omega) = \frac{1}{\sqrt{1 + (\omega RC)^2}e^{j \ atan(\frac{\omega RC}{1})}} = \frac{1}{\sqrt{1 + (\omega RC)^2}}e^{-j \ atan(\omega RC)}
The magnitude and phase of
H are,
|H| = \frac{1}{\sqrt{1 + (\omega RC)^2}}
\angle H = \theta_H = - atan(\omega RC)
Earlier I contended that if we want to find the sinusoidal steady-state analysis
vc(t), knowing that v_s(t) = Acos(\omega_0 t), it is simply
v_c(t) = A|H|cos(\omega_0 t + \theta_H)
And I think that's what your question is about. Correct me if I'm wrong, but I think you were originally asking, 'where does the phase shift come from -- mathematically speaking?' To answer that, we need to convert v_s (t) = cos(\omega_0 t) to the frequency domain -- not just its symbol, V_s(\omega) -- but the
whole thing. And we can do that using the Fourier transform. This is where it gets fun (or if you wish, phun

). I suggest you work through this at least once. You may never have to do it again for sinusoidal steady-state analysis, but going though it will answer your questions.
We define the Fourier transform and inverse Fourier transform as,
X(\omega) = F\{x(t)\} = \int _{-\infty} ^{\infty} x(t) e^{-j \omega t} dt
x(t) = F^{-1} \{X(\omega)\} = \frac{1}{2 \pi}\int _{-\infty} ^{\infty} X(\omega) e^{j \omega t} d\omega
Please note that these are not the only way to define the Fourier transform and inverse! In another way to define them, instead of the 1/2 \pi in the inverse (like I used), a 1/\sqrt{2 \pi} is used in both the forward and inverse. In yet another way to define them, no terms are to the left of the integral, and a 2 \pi is in the exponential terms. The way I defined them here is very common in electrical engineering courses. But it is not absolute. I highly suggest using the definition that your textbook/coursework uses, whatever that may be.
The Fourier trasform of v_s(t) [/tex] in our circuit is,<br />
<br />
V_s(\omega) = \int _{-\infty} ^{\infty} A \ cos(\omega_0 t)e^{-j \omega t} = \pi A \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right)<br />
<br />
where \delta() is the Dirac delta function (sometimes called the <i>impulse function</i>, and sometimes simply the <i>delta function</i>). Now you might be asking, "where in the world did he get that?" Honestly, the above integral is a little tricky to do explicitly, and it involves some reformulation of the integral, then taking some limits and such. But if you want a weak proof, take the inverse Fourier transform of \pi A \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right) and you'll find it easily produces A \ cos(\omega_0 t).<br />
<br />
Recall <br />
<br />
V_c(\omega) = H(\omega)V_s(\omega)<br />
<br />
= \frac{1}{\sqrt{1 + (\omega RC)^2}}e^{-atan(\omega RC)} \pi A \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right)<br />
<br />
Thus,<br />
<br />
V_c(\omega) = \frac{\pi A}{\sqrt{1 + (\omega RC)^2}} \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right) e^{-j \ atan(\omega RC)}<br />
<br />
Now let's take the inverse Fourier transform. <br />
<br />
v_c(t) = \frac{1}{2 \pi} \int _{-\infty} ^{\infty} \frac{\pi A}{\sqrt{1 + (\omega RC)^2}} \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right) e^{-j \ atan(\omega RC)}e^{j \omega t} d \omega<br />
<br />
= \frac{A}{2} \int _{-\infty} ^{\infty} \frac{1}{\sqrt{1 + (\omega RC)^2}} \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right) e^{j \left( \omega t - atan(\omega RC) \right)} d \omega<br />
<br />
Noting that \int f(x)\delta(x - x_0)dx = f(x_0), the integral evaluates to<br />
<br />
v_c(t) = \frac{A}{2 \sqrt{1 + (\omega_0 RC)^2}} \left(e^{j(\omega_0 t - atan(\omega_0 RC))} + e^{-j(\omega_0 t - atan(\omega_0 RC))} \right)<br />
<br />
= \frac{A}{\sqrt{1 + (\omega_0 RC)^2}} cos \left( \omega_0 t - atan(\omega_0 RC) \right)<br />
<br />
thus for sinusoidal steady-state analysis,<br />
<br />
v_c(t) = A|H|cos(\omega_0 t + \theta_H)<br />
<br />
And that's where the phase shift comes from! <img src="https://cdn.jsdelivr.net/joypixels/assets/8.0/png/unicode/64/1f600.png" class="smilie smilie--emoji" loading="lazy" width="64" height="64" alt=":biggrin:" title="Big Grin :biggrin:" data-smilie="8"data-shortname=":biggrin:" />