Solving Principle of Moments: F1 & F2

[Cain]

Hello,
This is probably really simple but i don't know if this is the right way to work out the answer
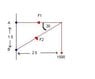
i have attached an image containing the problem.

I know how to get F2 :
Taking moments about A:
F2 Cos 60 = 1500
F2 = 3000N

But then it says to find F1 using the principle of moments, and the only way i can get the answer is:
taking moments about B: (F1 x 1.5) = (1500 x 2.5)
F1 = (1500 x 2.5) / 1.5
F1 = 2500N

is this right?

Thanks alot
Cain

 

[Mindscrape]

Well, you can check your answer by just using trig like you did earlier.
F_1 = F_{2}*cos(30) = 1500*sqrt{3}

You fell into the unfortunate trap of notation. The definition of a moment is that M = B x r, which shows us that the moment is the cross product of the vector and the scalar where the vector is applied. You should go back and nail down the concept of moments, then try the problem out again.

 

[civil_dude]

Your original equation is not right.

To sum moments, you need a force AND a distance, i.e. F2 (cos 60) * 1.5 = 1500 * 2.5.