Alex.malh
- 17
- 0
Homework Statement
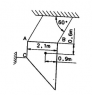
A plate is fixed to the ceiling by two wires and to the wall by a single wire.
The wall wire is cut. Calculate the tension in the two remaining wires.
mass = 800 kg
g = 10m/s²
Dimensions in sketch
Homework Equations
The Attempt at a Solution
Equations:
Ra*cos30 + Rb*cos30 = m*g + m*av
Ra*sin30 + Rb*sin30 = -m*ah
ah*sin30/cos30 = av
Solve to:
(Ra+Rb)=6928N
ah=-4.33m/s²
av=-2.5m/s²
But now I'm having troubles getting the individual wire tensions.
Any help is welcome.
Thank you.