Static Equilibrium Pulley Problem

[Sixth42]

Homework Statement

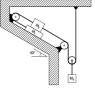
The attachment above contains the diagram given in the problem

M₁ = 25kg
M₂ = 35kg
Friction coefficient between M₁ and stucture = 0.15
Friction coefficient between M₁ and M₂ = 0.25
Friction on pulleys and mass on pulleys is negligible.

Find the minimum mass M₃ for sliding to occur in the system (i.e. the maximum mass for which the system will remain in static equilibrium).

Homework Equations

∑F_x = 0
ΣF_y = 0

The Attempt at a Solution

For the first mass:

The above attachment contains the diagram I used with the rotated coordinate system. My equations were:
∑F_y = 0
-M₂g sin(60°)-M₁g sin(60°) + Fn = 0
Fn = 509.7N

∑F_x = 0
-M₂g cos(60°)-M₁g cos(60°) - 0.15Fn + T₁ = 0
T₁ = 370.8N

For the second mass:

The above attachment contains the diagram I used with the rotated coordinate system. My equations were:
∑F_y = 0
-M₂g sin(60°) + Fn₂ = 0
Fn₂ = 297.3N

∑F_x = 0
-M₂g cos(60°) - 0.25Fn₂ - T₂ + T₁ = 0
T₂ = 124.8N

For the pulley attached to M3:

∑F_y = 0
2T₂ - M₃ = 0
M₃ = 249.6N

Therefore mass of M₃ = 249.6/9.81 = 25.44kg

I managed to get a final answer of M₃ = 25.44kg (or 249.6N) by working on each mass individually. Using a rotated coordinate system for M₁ and M₂. It would be nice if someone could confirm this answer for me but my main questions are:
Was I correct in adding M₂ to the force diagram for M₁?
In both diagrams, is the friction force in the correct direction?
Does this method look correct overall or did I miss something?

Thanks for the help.

 

[Chestermiller]

Your force balance that you identify as M1 is really the force balance on the combination of M1 and M2, and should be identified as such. Also, M2 should be shown on this free body diagram.

You analysis inherently assumes that the static friction between M1 with the incline, and M2 with M1 will occur at the same value of M3. This is not necessarily the case. One of these static frictions may release first, then causing the other to release when the forces readjust.

 

[Sixth42]

Thank you very much Chester, I see where it went wrong