Dieinhell100
- 13
- 0
Homework Statement
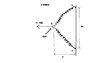
The springs BA and BC each have a stiffness of 500N/m and an unstretched length of 3m. Determine the displacement d of the cord from the wall when a force F = 175N is applied to the cord.
Homework Equations
F=ks
ƩFx=0
ƩFy=0
The Attempt at a Solution
This is as far as I got. I set out the sum of the forces in the x and y direction, assuming left is positive x and up is positive y. I don't know what to do from here with the information they have given me.
ƩFx=F-Tᴮᴬcosθ -Tᴮᶜcos(θ)=0
ƩFy=Tᴮᴬsinθ-Tᴮᶜsinθ=0
Tᴮᴬ=ks=500N/m * (l-3m)
Tᴮᶜ=ks=500N/m * (l-3m)
I'm not sure what to do when I don't have the angles or the stretched length. Attached is a drawing I made of the problem (excuse me for my messiness).