Amaelle
- 309
- 54
Good day all,
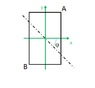
I have an issue regarding the theoretical concept regarding the stress generated by the skew bending
in a rectangular cross section for example

the formula used to calculated the stress is

while when it is a circular cross section we have the following formula

I really can't understand why we use different formulas in the second case (I couldn't understand the given explanations)
many thanks in advance
I have an issue regarding the theoretical concept regarding the stress generated by the skew bending
in a rectangular cross section for example
the formula used to calculated the stress is
while when it is a circular cross section we have the following formula
I really can't understand why we use different formulas in the second case (I couldn't understand the given explanations)
many thanks in advance
Attachments
Last edited by a moderator: