Symmetry breaking in the AdS small/large black hole phase transition

[codebpr]

TL;DR Summary

Which symmetry is being broken during a small/large AdS black hole phase transition using the Landau's phase transition approach?

I am trying to reproduce the results from this paper where they find out the expression for the Landau functional to be

$$\psi(x,t,p)=\frac{1}{4}(\frac{1}{x}+6x+px^3-4tx^2)$$

We plot the Landau functional v/s the order parameter($x$) at $p=0.5$ and obtain the Figure 4. from the paper as

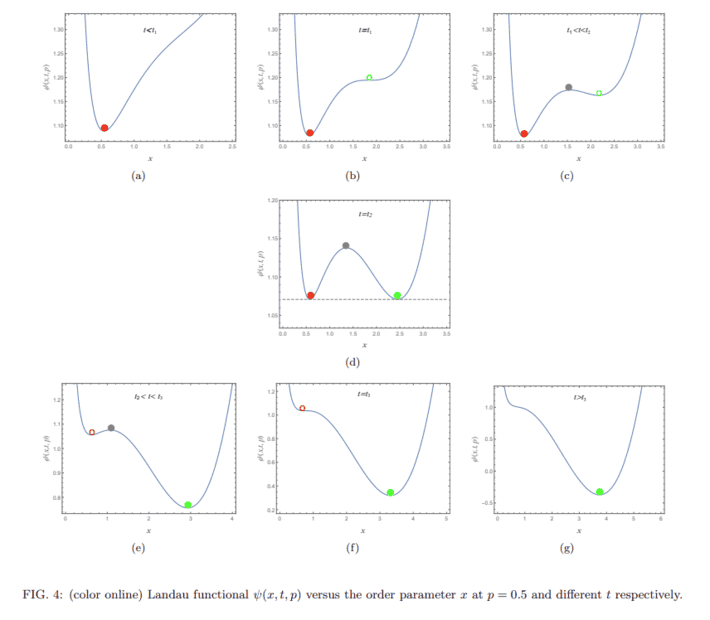
Now according to free energy approach, this is a first-order phase transition. According to Landau theory, every phase transition is related to a symmetry breaking. Which symmetry is being broken here, for this system of AdS black holes?

 

[DrDu]

At least with the van der Waals model, i.e. gas-liquid phase transition, there is no symmetry breaking associated with it. I think it is simply not true that every phase transition is related to a symmetry breaking.

 

[AndreasC]

At least with the van der Waals model, i.e. gas-liquid phase transition, there is no symmetry breaking associated with it. I think it is simply not true that every phase transition is related to a symmetry breaking.

Supposedly Landau theory only fails in that respect in some weird low temperature scenaria, but you are right that I can't really think of how the gas to liquid transition breaks a symmetry... I also can't seem to find it anywhere, maybe someone else knows...

 

[Demystifier]

Which symmetry is being broken here

One can answer this question formally, without understanding physics. Shift the variable $x$ such that the red minimum of the plotted function is at $x=0$. The minimum $x=0$ is hence invariant under the transformation $x\to -x$. The green minimum is not invariant under $x\to -x$, so the broken symmetry is the inversion $x\to -x$, for the shifted $x$.

 

[DrDu]

Hm, ok, but this is not a symmetry of the system or its hamiltonian.

 

[Demystifier]

Hm, ok, but this is not a symmetry of the system or its hamiltonian.

True, in general there is no any reason why the Landau functional should have any exact symmetry. But close to the minimum $x=x_{\rm red}$ the functional can be expanded
$$\psi(x,...)=a+b(x-x_{\rm red})^2+...$$
which at least has an approximate symmetry.

EDIT: Or maybe there is always some exact symmetry in the sense of Galois theory?
http://www.cc.kyoto-su.ac.jp/project/MISC/slide/seminar-s/2011/120112Takeuchi.pdf