- #1
mmmboh
- 407
- 0
Hi, this isn't homework, just a practice problem (for which the solution is given)I found online that I am trying to prepare for my midterm next week:
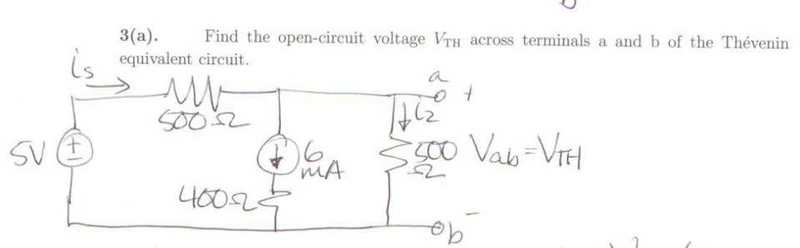
My question is why can't I simple solve for is using the left loop. So 5V-500is-400(6ma)=0, which gives is=5.2ma...alternatively I didn't really have to use KCL, I could have just said that the voltage around the loop must equal zero, so the voltage across the 500 ohm resistor is 5V-2.4V=2.6V, and that's what I would think the thevenin voltage is, but apparently it can't be done that way and the actual thevenin voltage is 1V. Would someone mind explaining this? I think I may be understanding this because I am misunderstanding current sources, can someone clear things up for me please?
Thank you.
My question is why can't I simple solve for is using the left loop. So 5V-500is-400(6ma)=0, which gives is=5.2ma...alternatively I didn't really have to use KCL, I could have just said that the voltage around the loop must equal zero, so the voltage across the 500 ohm resistor is 5V-2.4V=2.6V, and that's what I would think the thevenin voltage is, but apparently it can't be done that way and the actual thevenin voltage is 1V. Would someone mind explaining this? I think I may be understanding this because I am misunderstanding current sources, can someone clear things up for me please?
Thank you.