joshanders_84
- 23
- 0
This is another problem I am having troubles with. Here's the prompt:
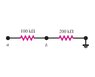
What is the reading of a voltmeter with the proper range and with resistance 5*10^4 Ohms when connected between point b and ground?
I know that for voltmeters, V = I_fs (R_c + R_s), and I tried solving for V using the I through the system as I_fs, which I solved as (400V/300000) = .001333, and then using 5*10^4 and 200000 as the resistors, but it says my answer is off by an additive constant. I don't understand what I am dong wrong...all help is appreciated. Thanks
Josh
What is the reading of a voltmeter with the proper range and with resistance 5*10^4 Ohms when connected between point b and ground?
I know that for voltmeters, V = I_fs (R_c + R_s), and I tried solving for V using the I through the system as I_fs, which I solved as (400V/300000) = .001333, and then using 5*10^4 and 200000 as the resistors, but it says my answer is off by an additive constant. I don't understand what I am dong wrong...all help is appreciated. Thanks
Josh