Two Stage Amplifier -- Find the Input Resistance

Thread starter IronaSona
Start date May 2, 2021
Tags

Amplifier Input Resistance

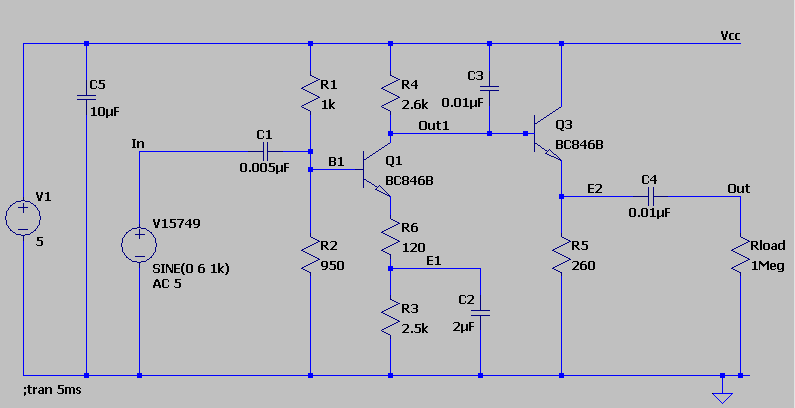
Click For Summary

The discussion focuses on determining the input resistance of a two-stage amplifier and the effects of feedback on this parameter. Participants are questioning the appropriate formula for calculating input resistance and discussing the role of feedback in the amplifier's design. There is mention of resistors R1 and R2 being in parallel with the input impedance of transistor Q1, which influences the overall input resistance. Clarification on the feedback mechanism within the amplifier is also sought. Understanding these elements is crucial for accurately analyzing the circuit's performance.

May 2, 2021

IronaSona

Homework Statement: .

Relevant Equations: .

Am trying to find Effects of Feedback - Input resistance of this circuit.
Is this the formula that in need to use to find the input resistance of this circuit ?

Physics news on Phys.org

May 2, 2021

berkeman

Admin

Where do you see feedback in this amp? And R1 and R2 are in parallel with the input impedance of Q1...

Thread 'Chain falling out of a horizontal tube onto a table'

My attempt: Initial total M.E = PE of hanging part + PE of part of chain in the tube. I've considered the table as to be at zero of PE. PE of hanging part = ##\frac{1}{2} \frac{m}{l}gh^{2}##. PE of part in the tube = ##\frac{m}{l}(l - h)gh##. Final ME = ##\frac{1}{2}\frac{m}{l}gh^{2}## + ##\frac{1}{2}\frac{m}{l}hv^{2}##. Since Initial ME = Final ME. Therefore, ##\frac{1}{2}\frac{m}{l}hv^{2}## = ##\frac{m}{l}(l-h)gh##. Solving this gives: ## v = \sqrt{2g(l-h)}##. But the answer in the book...

View full post »