Undetermined system for electric network

[arestes]

Hello!
First of all, this is not a HW problem and I already solved it. Actually, it most likely was a HW problem for my friend who gave it to me. I would take the opportunity to ask exactly how to handle this: I'm not a student but I like going back to school exercises in Physics and gain deeper understanding now. Should I always mention this? Should I take this to the homework forum to avoid raising (incorrect) suspicion (in which case i don't think I would get the appropriate response, which is to discuss rather than solve)?

Anyway: This system:

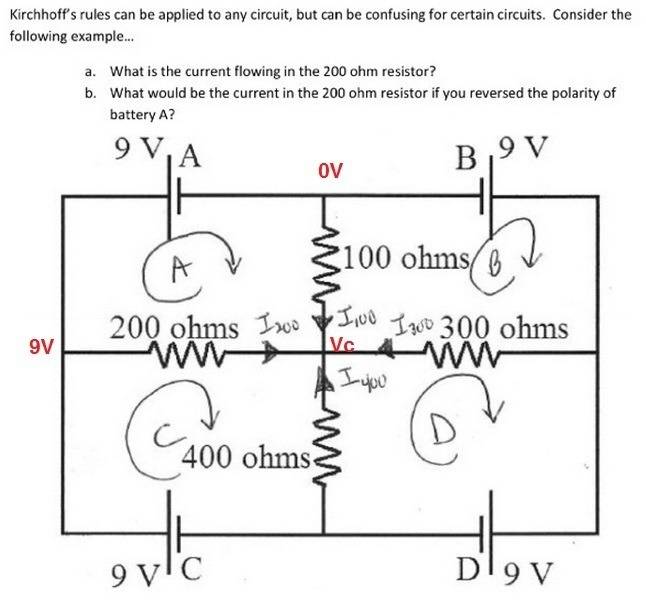
At first I tried to do it with the mesh currents circulating as shown and I found out the system is undetermined.
These are the mesh current equations for the four inner loops:
$$ 9=300 I_1 +100 I_2+200I_3+0I_4 \\
9=100 I_1 +400 I_2+ 0I_3+300I_4 \\
9=0 I_1 +300 I_2+400I_3+700I_4 \\
9=200 I_1 + 0 I_2+600I_3+400I_4 $$
There are infinitely many solutions!

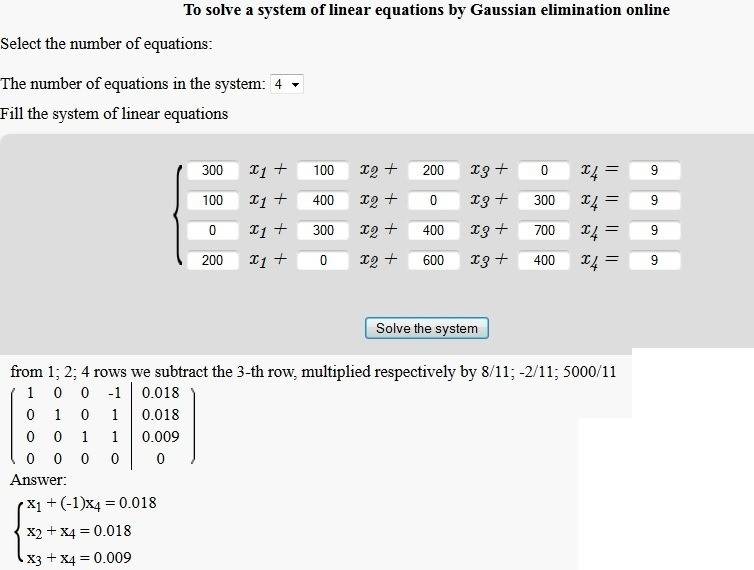
This is not the first time I came across this but it usually meant that I had forgotten to eliminate an extra nonexistent current.

However, I solved this by assigning actual (branch) currents going through each resistor and assigning an unknown voltage Vc to the central node and then applying Ohm's law. (I assigned a reference voltage of zero at the node between A and B).
$$ V_c=100i_1 \\
V_c=400 i_4\\
9-V_c=200 i_2\\
9-V_c=300 i_3\\
i_1+i_4=i_2+i_3$$

Solving this system I got that the currents are $i_1=36mA \quad i_2= 27 mA \quad i_3= 18 mA$ and $i_4=9mA$ with the central voltage $V_c=3.6 V$. This is the solution.
I am puzzled as to two things:
(A) What is the underlying reason the system formed by considering MESH CURRENTS (as drawn in the image) is undetermined: I recall this has happened to me when I could clearly see that there was a fictitious mesh current but here there are four, which is the same number of real currents.
(B) Moreover, these mesh currents are the ones the are supposed to get through the sources, they should MEAN something.
(C) I can see that this network has the four sources aligned such that they don't contradict each other with regards voltage. Part b. of the problem asks what happens if one of them is reversed. This would be a contradiction for voltages. I honestly don't know what would happen and my best guess is that it would break the batteries.

Any thoughts?
cheers

 

[NascentOxygen]

At first I tried to do it with the mesh currents circulating as shown and I found out the system is undetermined.

You haven't used mesh analysis. In truth, I can't figure out what you've done.

This is mesh analysis:

If we denote the mesh currents according to your labels, then around mesh A we have this voltage equation:
9 = 200(I_C - I_A) + 100(I_B - I_A)

Explanation: nett current through the 200Ω resistor flowing from L to R is I_C + -I_A

Now, do similar for the other 3 meshes.Then solve.

BTW, whenever you have 4 equations in 4 unknowns, I can't see it can't be solved so long as one equation is not identical with another. But it won't be the solution to this circuit analysis.

 

[arestes]

Hi!
I'm sorry, I just noticed something that might have confused you: I had drawn mesh currents the opposite way I used them for the equations (although the analysis would also be undetermined either way: I'm just changing directions of the variables and renaming them to subscript numbers as opposed to letters). I am attaching a diagram with the currents as I used them:

 

[NascentOxygen]

Repeating what I said in my first reply.

You haven't used mesh analysis. In truth, I can't figure out what you've done.

This is mesh analysis:

If we denote the mesh currents according to your labels, then around mesh 1 we have this voltage equation:
9 = 200(I₁ + I₃) + 100(I₁ + I₂)

Explanation: nett current through the 200Ω resistor flowing from L to R is I₁ + I₃

Now, do similar for the other 3 meshes. Then solve.

BTW, whenever you have 4 equations in 4 unknowns. I think it can be solved so long as one equation is not identical with another. But your equations still won't be the solution to this circuit analysis.

 

[Dale]

A better way would be to do node voltage analysis. There is only one unknown node voltage, so you get one equation in one unknown. I generally prefer node voltage over mesh current.

 

[arestes]

Hello DaleSpam. I have already solved the problem using node voltage analysis.
I am trying to discuss why mesh analysis fails here and also what happens in part b. That's why I didn't post it as homework because it isn't and I'm actually not even a student anymore.
Btw, this is not the first time I've come across failure of mesh analysis but I've always attributed it to not noticing that there was a fictitious mesh current that was unnecesary and introduced a redundancy in the equations.
However, there are an equal number of actual branch currents (using node voltage analysis) as there are mesh currents so I'm puzzled.
This is not homework, btw. Just trying to gain deeper understanding.

 

[arestes]

Today at 3:07 PM#4
https://www.physicsforums.com/members/nascentoxygen.336970/
Hello. I have alredy done what you say. I've been using mesh analysis all along correctly. I just skipped one step, but here it is complete, if you want to check. I am completely sure this is correct according to mesh analysis. I also happen to know that sometimes mesh analysis fails but everytime I've seen it fail I could attribute it to not noticing that there was a redundant mesh with an unphysical mesh current that could be eliminated from the beginning. I do't think this happens here because there's an equal number of mesh currents and branch currents and I've already solved the problem with node voltage analysis.

9 = 200(I1 + I3) + 100(I1 + I2) =300*I1+100 *I2 + 200*I3 (+obviously 0*I4) upper left mesh
9 = 300(I2 + I4) + 100(I1 + I2) =100*I1+400 *I2 (+obviously 0*I3)+ 300*I4 upper right mesh
9 = 300(I2 + I4) + 400(I3 + I4) =(+obviously 0*I1)+300*I2+400 *I3 + 700*I4 lower right mesh
9 = 200(I1 + I3) + 400(I3 + I4) =200*I1+(+obviously 0*I2)+600 *I3 + 400*I3 lower left mesh
Do you see now that they are the same equations?

I just want to discuss why this fails here.

 

[jbriggs444]

BTW, whenever you have 4 equations in 4 unknowns. I think it can be solved so long as one equation is not identical with another. But your equations still won't be the solution to this circuit analysis.

A system of n simultaneous linear equations in n unknowns can have a unique solution only if the equations are linearly independent. That is, none of the equations can be obtainable as a linear combination of the others. If the equations are linearly independent and are not inconsistent then a unique solution will exist.

 

[Dale]

this is not the first time I've come across failure of mesh analysis

Mesh current analysis is not as general as node voltage analysis. It fails for some circuit topologies. That is the main reason I prefer node voltage. That said, the topology looks fine so I am not sure why you had a problem. I will try to work it out later tonight and see if I run into the same problem.

 

[Dale]

Actually, looking at the circuit, the problem is not mesh current analysis, the problem is the circuit itself. The current through the voltage sources is indeterminate.

 

[arestes]

Actually, looking at the circuit, the problem is not mesh current analysis, the problem is the circuit itself. The current through the voltage sources is indeterminate.

Yes. However, We can obtain sensible answers for the currents going through each resistor by using node voltage analysis.
This is exactly why I'm puzzled. There are no definite values for the currents going through the sources but perfectly fine answers for the ones across the resistors.

Also, what happens if we invert the polarity of source A? does the circuit explode or what?

 

[NascentOxygen]

It's an impractical circuit, indeed. Unless the voltage sources are all exactly equal there will be an infinite current circulating through them (assuming ideal sources). It's a case of arranging voltage sources in parallel, they need to be exactly equal since there is no resistance to limit current.

 

[Dale]

Yes. However, We can obtain sensible answers for the currents going through each resistor by using node voltage analysis.
This is exactly why I'm puzzled. There are no definite values for the currents going through the sources but perfectly fine answers for the ones across the resistors.

Yes, that is what you get for the mesh current analysis also. There are definite values for the currents through the resistors, but not for the currents through the sources. The only difference is that in mesh current analysis those indefinite currents are the variables that you have chosen. So you cannot solve for those variables, but only for their sums.

Also, what happens if we invert the polarity of source A? does the circuit explode or what?

You cannot invert the polarity of A, it is a self-contradiction.

 

[Dale]

There are no definite values for the currents going through the sources but perfectly fine answers for the ones across the resistors.

So if you express the equations in a matrix form, then you find that the rank of the matrix is 3, meaning that there are only 3 linearly independent equations. You can solve the equations for (B-A), (C-A), and (D-A), all of which are sensible and finite and from which you can get all of the currents through the resistors. But A remains completely indeterminate, any value for A leads to a valid set of solutions with the same current through the resistors but different currents through the sources.

 

[arestes]

So if you express the equations in a matrix form, then you find that the rank of the matrix is 3, meaning that there are only 3 linearly independent equations. You can solve the equations for (B-A), (C-A), and (D-A), all of which are sensible and finite and from which you can get all of the currents through the resistors. But A remains completely indeterminate, any value for A leads to a valid set of solutions with the same current through the resistors but different currents through the sources.

Yes. We agree in everything mathematically. I would like to know what's going on physically.
For example: I've seen cases in which mesh analysis fails because there was a loop that didn't actually exist (rearranging the wires fixed it). But here there are four mesh currents but also four branch currents. I don't see redundancy.

 

[NascentOxygen]

It's an interesting arrangement, presumably designed as a trick question. Only 3 voltage sources are needed, the 4th just confirms the voltage set by the other 3 (and that 4th one must be an exact match otherwise infinite currents circulate around the outer loop of sources with no limiting resistance).

So we can leave out, say, source D because that corner's voltage is set by the other 3 sources, anyway. So it's actually a circuit of just 3 meshes.

Solving for the currents when redundant source D is omitted, I get I1=18mA, I2=18mA, I3=9mA. This should give the same resistor currents as the original, and the centre node is still 3.6V.

So in summary, it's a circuit of 3 meshes, but where someone has decided to confound analysis by throwing in an additional source of potential matching exactly that already existing between those points.

 

[ME_student]

Just out of curiosity, but why don't you draw all the loops either counterclockwise or clockwise? Don't complicate the analysis for yourself too much. (haha)

 

[Dale]

Yes. We agree in everything mathematically. I would like to know what's going on physically.

What is going on physically is that the approximations that we typically make are not valid approximations in this case. Specifically, we usually approximate a voltage source as having zero impedance and we usually approximate the wires as having zero resistance.

That usually doesn't cause a problem because usually their impedance is small compared to that of the other elements in the path. But in this case it leads to a non-physical closed loop of zero impedance through all of the sources.

Are you familiar with superposition for solving circuits? If so, then look at the circuit in that context.

 

[epenguin]

Is the answer for part a that all the currents are zero, everywhere you have equal potentials opposing each other, directly or through resistors and your linear algebra is only ever going to give you the famous 'trivial solution?

Edit : OK it's wrong to say currents are zero. They are non-zero and perfectly definite in the 'cross' I think . (Just one of these now-you-see-it now-you-don't attempts to see simplification.) The problem must be the unphysical idealisation that has been pointed out, making how the current divides itself in the battery branches indeterminate. If you put a small resistance equal for all the batteries it should work out definite, and the ratio independent of its value as long as it is small.

 

[epenguin]

I think I've got it now. I will come back with a figure later when I have time but label top and bottom nodes A and B, side nodes C and D, central node O.

The question you have to ask is is it feasible that A and B are at exactly the same potential? I have assumed that A and B are directly connected (by a perfectly conducting wire). Then they are at the same potential. If you do not assume this then you can have only one reference potential at say A, call it 0, and then you have to calculate it at B and maybe it is not quite 0 necessarily? Haven't done this but... *

on my assumption you can fuse A and B into a single node, call it AB. You then have two parallel wires + batteries from AB to C (similarly to D). And normally you would presume in the ideal case equal current passes through them - though you wouldn't really care. But if you gave the batteries internal resistance then the current would distribute itself between the two parallel branches in inverse proportion to their resistances. However the total current AB to C is always the same and determined by the other resistances of the circuit as long as these are much greater than the battery resistances. You can have a lot of variability of internal resistances and so of the ratio of the two currents without affecting anything else so long as these resistances are small.

So I think the discomfort can be alleviated.

*Edit: ah yes, in the ideal case they are at same potential - A and B are separated by ideal perfect conductors with opposed equal batteries, like they were not there for this purpose. My construction was helpful to me bu may not be necessary.

 

[Tom_K]

This is a fun question! Looking at this thing, since the top and bottom are at equipotential as well as the left and right sides, it looks like it can be folded up like a napkin to get the equivalent circuit.
First, fold it over horizontally (along the vertical center line) so that the 200 ohm and 300 ohm resistors are in parallel. Now there are only two loops which can readily be solved for 36 ma through the 100 ohm resistor and 9 ma through the 400 ohm resistor.
Fold it again vertically so that the 100 and 400 ohm resistors are in parallel and all you have left is a 9 V battery in series with 200 ohm resistance with a total current draw of 45 ma, confirming the previous loop currents are correct.
Once that information is had the circuit can be unfolded again and the 4 loop currents are can be resolved with Ohm’s law as: 18 ma, 18 ma, 0 ma, 9 ma, going around clockwise from upper left for a total of 45 ma, as before.

 

[epenguin]

On right equivalent circuit I found helpful for understanding original circuit on left.

As explained in last post, the distribution of current between e.g. the two AB → C branches depends (inversely) on the battery resistances (not shown) in each of these branches, but as long as they are small the total of the two currents is constant.