JohnP60
- 6
- 0
Homework Statement
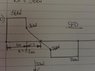
I have to work out the reactions at A & D. Sketch the shear force diagram for the beam and sketch the bending moment diagram.
i have worked out the reactions at A=56kN and D=34kN. I have done the SFD. I am just struggling doing the bending moment diagram and don't know how to work out the maximum bending moment.
Homework Equations
The Attempt at a Solution
RA + RD = 90kN
5RD = (20X1) + (60X2) + (10X3)
5RD = 170kN
RD = 34kN
RA=56kN.
I have done the SFD.
Bending moment diagram i have to state the three significant values.
I have left side as (56x1) = 56kN M
right hand side is (34x2) = 68kN M
i just don't know how to work out the maximum bending moment would appreciate any help