Varying fluid (density) in a cylinder rolling along an inclined plane

[mostafaelsan2005]

What does the 1.84 represent.

The kinematic viscosity $\nu=\mu/\rho$ is not in poise. It is in cm^2/sec. Dynamic viscosity $\mu$ is in poise. Watch your units!!!

Let's see the results for t or t/to vs the other dimensionless parameter involving kinematic viscosity.

No. The $\sqrt{3/2}$ comes from the asymptotic solution at large values of the dimensionless parameter involving kinematic viscosity.

The analytic solution at short times can't give 2.376. It has got to be close to 1. I need to see your calculated results for t/to vs the dimsionless parameter $\frac{\nu t_0}{\sqrt{\pi R^2}}$ for each of the fluids. One data point for each fluid.

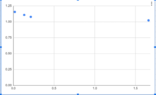
1.84 should represent the time it takes for water to reach the bottom of the ramp but that cannot be the case. I have done the calculation several times with a calculator and have gotten the same answer. It is weird that it comes out to 2.376, though, I thought that the value was supposed to be < < 1, is that not the case? Though I do note that in the solution you stated that it's much less than 1 for when we are calculating $sqrtvt/R$ and not $\frac{\nu t_0}{\sqrt{\pi R^2}}$ though I'm not quite sure of the difference and which one I should focus on. For the asymptotic solution at long times, how was sqrt(3/2) determined from the dimensionless parameters. On the section involving the dimensionless parameters I can't seem to find the derivation for it? I'll plot the rest of the values and see if there is any meaning to the data then using $\frac{\nu t_0}{\sqrt{\pi R^2}}$ for the other liquids I used.

 

[Chestermiller]

We lost something in transferring the results from post to post. The correct results are in post #45. The horizontal axis parameter should be $$\sqrt{\frac{\nu t_0}{\pi R^2}}$$ rather than $$\frac{\nu t_0}{\sqrt{\pi R^2}} $$

Try redoing the calculations with the correct parameter and let's see what you get. The incorrect parameter results should not have come out dimensionless.

Also, I’d like to see your calculations for the case of water.

 

[mostafaelsan2005]

We lost something in transferring the results from post to post. The correct results are in post #45. The horizontal axis parameter should be $$\sqrt{\frac{\nu t_0}{\pi R^2}}$$ rather than $$\frac{\nu t_0}{\sqrt{\pi R^2}} $$

Try redoing the calculations with the correct parameter and let's see what you get. The incorrect parameter results should not have come out dimensionless.

Also, I’d like to see your calculations for the case of water.

$\sqrt{\frac{\nu t_0}{\pi R^2}} = sqrt((1.29*0.01)/(pi*0.035^2)) = 1.83$. Any idea why this is the case (this is the calculation for water)? Also, for how you expressed the change in angular velocity over time in post #51, is there a source for this formula or is this from your own knowledge (the part before deriving the solution based on dimensionless parameters)? Would it be fair to say that I can omit the asymptotic solution and the solution of the dimensionless parameters from the investigation because an in-depth discussion into the viscosity boundary conditions and the parameters used to find the time taken to roll down the ramp should be sufficient based on my personal judgement, no? The only thing I would include perhaps is the derivation using the dimensionless parameters in the appendix so that I can refer to it in the theoretical background when I refer to how the long-time formula is:
$t=t_0*sqrt(3/2)$
Since the graphs I will include in the investigation will be based on the viscosity boundary conditions parameters that is what I based my personal judgement out of as to not let the theoretical background be too tedious for the examiner.
In that case, then is there a way that you derived the sqrt3/2 out of the dimensionless parameters because that it isn't explicitly mentioned how. I'm thinking of doing the experiment again today with more data points as it seems that the calculations aren't adding up, maybe they'll come out closer this time to the expression we have to calculate the time. I graphed the parameter as a function and you can see it here: https://www.desmos.com/calculator/fvlmni6hev
the calculations under the function and set hor. asymptotes and from top to bottom the fluids are: water, oil, honey, transmission fluid and as you can see the results are nonsensical. I'm not quite sure why this is happening (I am sure the calculations for the kinematic viscosity is correct as it is the viscosity in poise divided by the density of the liquid, maybe there is an issue in the densities? the numbers are ridiculously high

 

[Chestermiller]

$\sqrt{\frac{\nu t_0}{\pi R^2}} = sqrt((1.29*0.01)/(pi*0.035^2)) = 1.83$. Any idea why this is the case (this is the calculation for water)?

Yes. The units are screwed up. It should be 0.0183. The R should be 3.5, not 0.035. We are working with cgs.

Also, for how you expressed the change in angular velocity over time in post #51, is there a source for this formula or is this from your own knowledge (the part before deriving the solution based on dimensionless parameters)?

See Bird, Stewart, and Lightfoot, Transport Phenomena, Appendices

Would it be fair to say that I can omit the asymptotic solution and the solution of the dimensionless parameters from the investigation because an in-depth discussion into the viscosity boundary conditions and the parameters used to find the time taken to roll down the ramp should be sufficient based on my personal judgement, no? The only thing I would include perhaps is the derivation using the dimensionless parameters in the appendix so that I can refer to it in the theoretical background when I refer to how the long-time formula is:
$t=t_0*sqrt(3/2)$

This is a judgment call on your part. However, the derivation of the asymptotic solution is new, and has never appeared in the literature before. This would be a major contribution to the understanding and to the solution to this problem. You can take credit for it if you want. I don't care about being acknowledged.

Since the graphs I will include in the investigation will be based on the viscosity boundary conditions parameters that is what I based my personal judgement out of as to not let the theoretical background be too tedious for the examiner.

The theoretical development can be relegated to the Appendix. You can take credit for marshaling the resources to get the theoretical development implemented.

In that case, then is there a way that you derived the sqrt3/2 out of the dimensionless parameters because that it isn't explicitly mentioned how.

I don't follow. I thought I did this.

I'm thinking of doing the experiment again today with more data points as it seems that the calculations aren't adding up, maybe they'll come out closer this time to the expression we have to calculate the time. I graphed the parameter as a function and you can see it here: https://www.desmos.com/calculator/fvlmni6hev

I can't read the graph. t/to should be y, and the other dimensionless group should be x. Do you not have access to Microsoft Excel? In terms of these x and y parameters, the short term solution should be a straight line. $y=(1+\frac{16}{15}x)$

the calculations under the function and set hor. asymptotes and from top to bottom the fluids are: water, oil, honey, transmission fluid and as you can see the results are nonsensical. I'm not quite sure why this is happening (I am sure the calculations for the kinematic viscosity is correct as it is the viscosity in poise divided by the density of the liquid, maybe there is an issue in the densities? the numbers are ridiculously high

Like I said, the 0.035 should be 3.5.

 

[mostafaelsan2005]

Yes. The units are screwed up. It should be 0.0183. The R should be 3.5, not 0.035. We are working with cgs.

See Bird, Stewart, and Lightfoot, Transport Phenomena, Appendices

This is a judgment call on your part. However, the derivation of the asymptotic solution is new, and has never appeared in the literature before. This would be a major contribution to the understanding and to the solution to this problem. You can take credit for it if you want. I don't care about being acknowledged.

The theoretical development can be relegated to the Appendix. You can take credit for marshaling the resources to get the theoretical development implemented.

I don't follow. I thought I did this.

I can't read the graph. t/to should be y, and the other dimensionless group should be x. Do you not have access to Microsoft Excel? In terms of these x and y parameters, the short term solution should be a straight line. $y=(1+\frac{16}{15}x)$

Like I said, the 0.035 should be 3.5.

I redid the calculations then and the range of values is 0.0183-0.2087. Also, I was graphing the parameter for $t=\sqrt{\frac{\nu t_0}{\pi R^2}}$ not $t=t_0\left(1+\frac{16}{15}\frac{\nu t_0}{\sqrt{\pi R^2}}\right)$. In regards to the dimensionless parameters, I read it quite a few times to determine where the sqrt(3/2) came from but it was never explicitly stated in the post, I may have misunderstood it though or maybe it was inferred piece of information?

 

[Chestermiller]

I redid the calculations then and the range of values is 0.0183-0.2087. Also, I was graphing the parameter for $t=\sqrt{\frac{\nu t_0}{\pi R^2}}$ not $t=t_0\left(1+\frac{16}{15}\frac{\nu t_0}{\sqrt{\pi R^2}}\right)$.

The correct equation for short time behavior is $$t=t_0\left(1+\frac{16}{15}\sqrt{\frac{\nu t_0}{\pi R^2}}\right)$$You should be plotting the data points as $y=t/t_0$ vs $x=\sqrt{\frac{\nu t_0}{\pi R^2}}$

In regards to the dimensionless parameters, I read it quite a few times to determine where the sqrt(3/2) came from but it was never explicitly stated in the post, I may have misunderstood it though or maybe it was inferred piece of information?

Post #53 shows that the asymptotic viscous case acceleration of the center of mass at long times is $$a=\frac{2}{3}g\sin{\alpha}$$This compares with the inviscid case center of mass acceleration of $$a=g\sin{\alpha}$$Note that the asymptotic long time viscous case acceleration is 3/2 the inviscid case acceleration. The time to roll down the ramp is inversely proportional to the square root of the acceleration. So at very long times, the time to roll down the ramp for the viscous case is $\sqrt{3/2}$ the time for the inviscid case.

 

[mostafaelsan2005]

The correct equation for short time behavior is $$t=t_0\left(1+\frac{16}{15}\sqrt{\frac{\nu t_0}{\pi R^2}}\right)$$You should be plotting the data points as $y=t/t_0$ vs $x=\sqrt{\frac{\nu t_0}{\pi R^2}}$

Post #53 shows that the asymptotic viscous case acceleration of the center of mass at long times is $$a=\frac{2}{3}g\sin{\alpha}$$This compares with the inviscid case center of mass acceleration of $$a=g\sin{\alpha}$$Note that the asymptotic long time viscous case acceleration is 3/2 the inviscid case acceleration. The time to roll down the ramp is inversely proportional to the square root of the acceleration. So at very long times, the time to roll down the ramp for the viscous case is $\sqrt{3/2}$ the time for the inviscid case.

I see, that makes much more sense when speaking about the factor 3/2 in terms of the acceleration. In terms of the equation for the short time behavior, we know that $t_0$ is 1.29; however, what would I be inputting as $t$ in the equation to divide by $t_0$? I just want to make sure if that is the actual time it takes for the cylinder to reach the bottom of the ramp (based on the fluid within)

 

[Chestermiller]

I see, that makes much more sense when speaking about the factor 3/2 in terms of the acceleration. In terms of the equation for the short time behavior, we know that $t_0$ is 1.29; however, what would I be inputting as $t$ in the equation to divide by $t_0$? I just want to make sure if that is the actual time it takes for the cylinder to reach the bottom of the ramp (based on the fluid within)

If you are plotting the data points, then in t/to, you put the actual measured time down the ramp for t, and the inviscid time 1.29 sec, for to.

The plot should crudely look something like this:

 

[mostafaelsan2005]

If you are plotting the data points, then in t/to, you put the actual measured time down the ramp for t, and the inviscid time 1.29 sec, for to.

The plot should crudely look something like this:
View attachment 335775

Using the values of kinematic viscosities of

0.01 (water)

0.53 (sunflower oil)

82.75 (molasses honey)

1.37 (transmission fluid)

Based on these values, I got these data points for the liquids in the same order:

1.155	0.018
1.108	0.133
1.023	1.66
1.077	0.214

I cannot make any sense of these numbers as they are nowhere near the boundaries (1.29 to 1.57). The graph looks like this (only the points attached below). Why do you think that the graph looks like this? I am using the value of 3.5 cm as the radius and the others are constant values.

 

[Chestermiller]

Using the values of kinematic viscosities of

0.01 (water)

0.53 (sunflower oil)

82.75 (molasses honey)

1.37 (transmission fluid)

Based on these values, I got these data points for the liquids in the same order:

1.155	0.018
1.108	0.133
1.023	1.66
1.077	0.214

I cannot make any sense of these numbers as they are nowhere near the boundaries (1.29 to 1.57). The graph looks like this (only the points attached below). Why do you think that the graph looks like this? I am using the value of 3.5 cm as the radius and the others are constant values.

I have no idea what the numbers in the columns represent or how they were obtained. Please provide a sample calculation for the sunflower oil data point.

 

[mostafaelsan2005]

I have no idea what the numbers in the columns represent or how they were obtained. Please provide a sample calculation for the sunflower oil data point.

Sure, based on the kinematic viscosity of sunflower oil being approximately 0.53, then using $\sqrt{\frac{\nu t_0}{\pi R^2}}$, which is sqrt(0.53*1.29/pi*3.5^2) = 0.133288.

 

[mostafaelsan2005]

Sure, based on the kinematic viscosity of sunflower oil being approximately 0.53, then using $\sqrt{\frac{\nu t_0}{\pi R^2}}$, which is sqrt(0.53*1.29/pi*3.5^2) = 0.133288.

Could this be an issue with the values for kinematic viscosity? The values calculated are correct but perhaps the poise values used for the viscosity and/or the density values calculated have some issue unless the equation could somehow not be correct for this situation? Is there another way to calculate it?

 

[mostafaelsan2005]

I have no idea what the numbers in the columns represent or how they were obtained. Please provide a sample calculation for the sunflower oil data point.

I've been tweaking the numbers for some time now and I've come to the conclusion that even if the values for kinematic viscosity were such that we get the expected value from the boundary condition parameter, its values would not make sense theoretically based on the actual liquid. Is there something we're missing?

 

[Chestermiller]

Let’s see your graph.

 

[mostafaelsan2005]

This graph shows the viscosity boundary condition parameter where the kinematic viscosity is x in order to show the general shape of the curve. I've highlighted the first data point where x (kinematic viscosity) is 0.01 and you can see that the value is 0.018 which does not make sense in the context of the experiment.

 

[Chestermiller]

View attachment 336672
This graph shows the viscosity boundary condition parameter where the kinematic viscosity is x in order to show the general shape of the curve. I've highlighted the first data point where x (kinematic viscosity) is 0.01 and you can see that the value is 0.018 which does not make sense in the context of the experiment.

I can't see a thing from your photo.. Print it out and then take the photo.

 

[mostafaelsan2005]

I can't see a thing from your photo.. Print it out and then take the photo.

This is a scatterplot of what we find when graphing t/t_0 against the viscosity boundary condition parameter with data points that I have outlined in post #109. As you can see, there is little meaning attached to these data points as they are outside of the boundary conditions set. I have made sure to keep the radius in centimeters although it doesn't change much if it is in meters as the results still do not add up. I can add the asymptotes for the time into this graph, but it is surpassing it from both the minimum and maximum so it would not add anything.

 

[Chestermiller]

This is a scatterplot of what we find when graphing t/t_0 against the viscosity boundary condition parameter with data points that I have outlined in post #109. As you can see, there is little meaning attached to these data points as they are outside of the boundary conditions set. I have made sure to keep the radius in centimeters although it doesn't change much if it is in meters as the results still do not add up. I can add the asymptotes for the time into this graph, but it is surpassing it from both the minimum and maximum so it would not add anything.

This doesn't make any sense to me. Please make me a table of the times vs the kinematic viscosities. Previously, in your experiments, the shortest time was water and the longer times were the more viscous fluids.

 

[mostafaelsan2005]

	Density () ± 0.6 gcm3	Viscosity () in poise (approximated)	Kinematic viscosity ()
Water	1.0	0.01	0.01
Sunflower oil	0.92	0.49	0.53
Molasses honey	1.45	120.00	82.75
Transmission fluid	0.87	1.20	1.37

	Average time taken to reach bottom of ramp (s) ± 0.03 seconds
Water	1.49
Sunflower oil	1.43
Molasses honey	1.32
Transmission fluid	1.39

 

[Chestermiller]

	Density () ± 0.6 gcm3	Viscosity () in poise (approximated)	Kinematic viscosity ()
Water	1.0	0.01	0.01
Sunflower oil	0.92	0.49	0.53
Molasses honey	1.45	120.00	82.75
Transmission fluid	0.87	1.20	1.37

	Average time taken to reach bottom of ramp (s) ± 0.03 seconds
Water	1.49
Sunflower oil	1.43
Molasses honey	1.32
Transmission fluid	1.39

The time to roll down the ramp was largest for water and decreased monotonically with increasing kinematic viscosity. This is the exact opposite of the results in your original experiments. Why?

 

[mostafaelsan2005]

The time to roll down the ramp was largest for water and decreased monotonically with increasing kinematic viscosity. This is the exact opposite of the results in your original experiments. Why?

I did the experiments again, remember? I found that the results at first weren't accurate due to the lubrication of the ramp I was using. Once I did them again, and made sure that the ramp was not lubricated, I found this to be the set of values for the average time to go down the ramp. If it is needed, I can redo the experiment as I have all the equipment currently. Is the problem with the water data point?

small edit: Ill do the experiment again for all the data values, it should take me about 30 minutes or so and Ill relay the information. I'm not sure why the nearly inviscid liquid is coming out to be that with the highest time while the most viscous was the fastest. From what I understand theoretically, it should be the opposite due to less fluid resistance, right?

 

[Chestermiller]

I did the experiments again, remember? I found that the results at first weren't accurate due to the lubrication of the ramp I was using. Once I did them again, and made sure that the ramp was not lubricated, I found this to be the set of values for the average time to go down the ramp. If it is needed, I can redo the experiment as I have all the equipment currently. Is the problem with the water data point?

It is with the order of the points with respect to kinematic viscosity. Water should be the shortest time, and the time should increase monotonically with the kinematic viscosity of the fluid. In the original set of data, the time for water was only about 1.3 sec.

 

[mostafaelsan2005]

It is with the order of the points with respect to kinematic viscosity. Water should be the shortest time, and the time should increase monotonically with the kinematic viscosity of the fluid. In the original set of data, the time for water was only about 1.3 sec.

Apologies for the late response, I conducted the experiment again and I measured the times through 5 trials. Here are the average values for time:

Average time taken to reach bottom of ramp (s) ± 0.03 seconds
Water	1.33
Sunflower oil	1.35
Molasses honey	1.48
Transmission fluid	1.39

I'm not sure why there was a discrepancy in values but I have the suspicion that the timer I used in the previous set of data was damaged in some way. Here the value for water is coming out similar to the first conducted experiment so this set of data is the most accurate of the three with a functioning timer and minimal lubrication of the ramp.

 

[Chestermiller]

Apologies for the late response, I conducted the experiment again and I measured the times through 5 trials. Here are the average values for time:

Average time taken to reach bottom of ramp (s) ± 0.03 seconds
Water	1.33
Sunflower oil	1.35
Molasses honey	1.48
Transmission fluid	1.39

I'm not sure why there was a discrepancy in values but I have the suspicion that the timer I used in the previous set of data was damaged in some way. Here the value for water is coming out similar to the first conducted experiment so this set of data is the most accurate of the three with a functioning timer and minimal lubrication of the ramp.

Let’s see the graph now

 

[mostafaelsan2005]

Let’s see the graph now

The graph won't change though? The changing variable in the viscosity boundary condition parameter is the kinematic viscosity which is the same as I've said in Post #119.

 

[Chestermiller]

The graph won't change though? The changing variable in the viscosity boundary condition parameter is the kinematic viscosity which is the same as I've said in Post #119.

Of course it will. The times are different.

 

[mostafaelsan2005]

Of course it will. The times are different.

It has the same general shape but the values for t/t_0 are just different:

 

[Chestermiller]

What the hell are you talking about? This is not the same general shape at all. Now draw the two asymptotic approximations on this same graph for comparison.

 

[mostafaelsan2005]

What the hell are you talking about? This is not the same general shape at all. Now draw the two asymptotic approximations on this same graph for comparison.

The asymptotic approximations for t/t_0 will range from 1 to 1.217, correct? Otherwise it will be outside the boundary. Minimum = 1.29/1.29 and maximum = 1.57/1.29.

 

[Chestermiller]

The asymptotic approximations for t/t_0 will range from 1 to 1.217, correct? Otherwise it will be outside the boundary. Minimum = 1.29/1.29 and maximum = 1.57/1.29.

The asymptotes are y = 1.224 and $y=1+\frac{16}{15}x$, where $$y=\frac{t}{t_0}$$and $$x=\sqrt{\frac{\nu t_0}{\pi R^2}}$$

 

[Chestermiller]

The asymptotes are y = 1.224 and $y=1+\frac{16}{15}x$, where $$y=\frac{t}{t_0}$$and $$x=\sqrt{\frac{\nu t_0}{\pi R^2}}$$