Voltage, electric field and potential energy for concentric shells

AI Thread Summary
The discussion revolves around calculating the voltage, electric field, and potential energy at the center of two concentric shells, where shell A is charged at 120V and shell B is grounded at 0V. The initial assumption is that the voltage at the center (V0) equals 120V, but there is uncertainty regarding the electric field and potential energy values, with suggestions that the electric field (E0) might be zero. Participants request clarification on the geometry of the shells and the integral used for calculating the electric field. The conversation emphasizes the need for a precise problem statement and detailed attempts to solve the equations.
tinesi
Messages
2
Reaction score
0
aa.png


1. Homework Statement
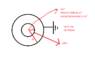
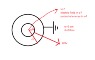
the a shell is charged Va=120v
shell b is grounded, Vb=0V

What is the voltage in the center of shells (vo)?
The electric field in the center of shells?
The potential energy in the center of shells?

Homework Equations


Vr=Va+(1/r-1/a)/(1/a-1/b)Vab (from integrals)
though I am not sure

The Attempt at a Solution


I assume that V0=Va=120V but I don't think so
I assume the field inside is 0

1/ro=1/0=0(?)
Vab=120v?
vo=-120v?
Eo=0?
U=0?
 

Attachments

  • aa.png
    aa.png
    5.1 KB · Views: 841
  • aa.png
    aa.png
    5.1 KB · Views: 981
Last edited:
Physics news on Phys.org
You have not reproduced a proper problem statement. Please spell out the problem exactly as given and give your detailed attempt.
 
Sorry, my first time here. I have written more details.
 
Welcome to the PF. :smile:
tinesi said:

Homework Statement


the a shell is charged Va=120v
shell b is grounded, Vb=0V

What is the voltage in the center of shells (vo)?
The electric field in the center of shells?
The potential energy in the center of shells?
Are the concentric shells spherical or cylindrical? Can you show the integral that is used to calculate the E-field for this geometry?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Minimizing the Energy of Two Conductors Very Far Apart
Replies
23
Views
1K
Single Loop Potential difference -- sign issue
Replies
8
Views
1K
Capacitance of three concentric shells
Replies
3
Views
1K
The electric field inside a hole inside a conductor is still 0?
Replies
2
Views
2K
Electric Potential Difference -- Conceptual Question
Replies
6
Views
2K
Why are the electrostatic field lines normal to a charged conductor?
Replies
10
Views
1K
Why does electric potential energy increase if you move against the field?
Replies
6
Views
1K
Electric field at (0,0) for this charged square conductor
Replies
8
Views
2K
Potential difference between two points in an electric field
Replies
1
Views
2K
Magnetization of a paramagnetic sphere
Replies
11
Views
1K

Hot Threads

Recent Insights

Back
Top