riseofphoenix
- 294
- 2
What is the equivalent capcitance of this circuit! -- Figured it out.
I have a Physics final exam in 2 hours and I'm re-reviewing things...
This problem DOESN'T make any sense!
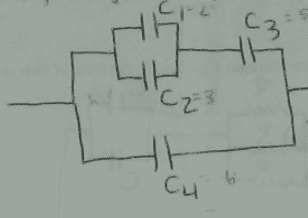
17. If C1 = 2 F, C2 = 3 F, C3 = 5 F, C4 = 6 F, the equivalent capacitance of the circuit is:
A. 8.5 F is supposed to be the answer - that makes NO sense
B. 16 F
C. 5.5 F
D. 10 F
I didn't get ANY of those numbers...
This is what I did.
1) Determine PARALLEL capacitance of C1 and C2
Ceq = C1 + C2
Ceq = 2 +3
Ceq = 5
2) Determine the SERIES capacitance of the whole circuit now
1/Ceq = 1/5 + 1/C3 + 1/C4
1/Ceq = 1/5 + 1/5+ 1/6
1/Ceq = 0.567
Ceq = 1/0.567
Ceq = 1.763 :(:(:(:(!Edit:
Oh wait nvm.
I figured it out.
the upper arm (C net) is- 1/C net = 1/5 + 1/C3 = 1/5 + 1/5 =2/5
=>C net = 5/2 = 2.5
now 2.5 and 6 in parallel- 2.5+6 = 8.5
I have a Physics final exam in 2 hours and I'm re-reviewing things...
This problem DOESN'T make any sense!
17. If C1 = 2 F, C2 = 3 F, C3 = 5 F, C4 = 6 F, the equivalent capacitance of the circuit is:
A. 8.5 F is supposed to be the answer - that makes NO sense
B. 16 F
C. 5.5 F
D. 10 F
I didn't get ANY of those numbers...
This is what I did.
1) Determine PARALLEL capacitance of C1 and C2
Ceq = C1 + C2
Ceq = 2 +3
Ceq = 5
2) Determine the SERIES capacitance of the whole circuit now
1/Ceq = 1/5 + 1/C3 + 1/C4
1/Ceq = 1/5 + 1/5+ 1/6
1/Ceq = 0.567
Ceq = 1/0.567
Ceq = 1.763 :(:(:(:(!Edit:
Oh wait nvm.
I figured it out.
the upper arm (C net) is- 1/C net = 1/5 + 1/C3 = 1/5 + 1/5 =2/5
=>C net = 5/2 = 2.5
now 2.5 and 6 in parallel- 2.5+6 = 8.5
Last edited:
 because this is stream of consciousness thinking for a quiz.
because this is stream of consciousness thinking for a quiz.