ClearWhey
- 19
- 4
- Homework Statement
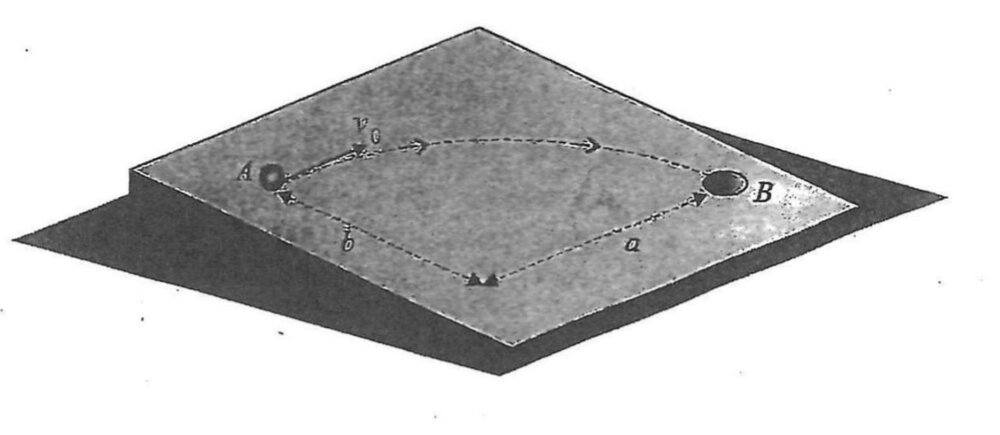
- A particle is at point A in a certain moment. The particle rolls with an angle of inclination a. It’s velocity direction is parallel to the upper edge. What velocity V0 does it need to reach into the hole B?
Sorry for my english
- Relevant Equations
- Look at the picture to get a better idea of the problem.
It was a long time ago I did these kind of problems so I’m a bit rusty. The only thing I can think of is divide it up to two parts one x and one y.
In y the acceleration is sin(a)*9.82? Then put that in the equation and solve for t.
In x the there is no acceleration so the formula is x=V0*t, I put in t from y and solve for V0?
Haven’t gotten the answer paper yet so I have no idea if I’m on the right path or wrong. That is why I’m asking here if I’m solving this question right, if not how should I do it?
Thanks in advance for the help!
In y the acceleration is sin(a)*9.82? Then put that in the equation and solve for t.
In x the there is no acceleration so the formula is x=V0*t, I put in t from y and solve for V0?
Haven’t gotten the answer paper yet so I have no idea if I’m on the right path or wrong. That is why I’m asking here if I’m solving this question right, if not how should I do it?
Thanks in advance for the help!