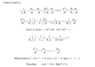paulmdrdo
- 89
- 2
- Homework Statement
- Find the expression for vo(t)
- Relevant Equations
- See the attached photo
I was trying to understand the way this problem was solved and I got confused with the latter part of the solution. I encircled the part that confused me. They seem to contradict each other. If dv(0+)/dt = 0 why is it dv(0+)/dt = -1 in the other one? Please explain. TIA!

http://i67.tinypic.com/t6s31y.jpg
http://i67.tinypic.com/t6s31y.jpg
Last edited: