Boundary Definition and 900 Threads
-
Graduate What is the purpose of applying a Dirichlet boundary condition?
Hi, If the dirichlet boundary condition is being applied, what does it tell us?- bluejay27
- Thread
- Boundary Boundary condition Condition
- Replies: 1
- Forum: Quantum Physics
-

Graduate Boundary condition for dielectric sphere
Is the potential across the boundary continuous for a dielectric sphere embedded in a dielectric material, so that the potential inside the sphere can be set equal to the potential outside of it at r=R ?- lonewolf219
- Thread
- Boundary Boundary condition Condition Dielectric Potential Sphere
- Replies: 2
- Forum: Electromagnetism
-
K
Undergrad What is the boundary surface of a collimator?
Hi everybody, I’m trying to calculate the shape of a boundary line f(x) between two mediums that collimates rays from a point light source. This requires the rays to hit the boundary line under a certain angle, so I calculated the slope m(φ) of the boundary line for a ray with polar angle φ (φ... -

MHB Can we just use a part of the boundary?
Hello! (Wave) We consider an elliptic operator $L$ in the space $\Omega$ with $c(x) \leq 0$. We suppose that $\partial{\Omega}=S_1 \cup S_2$. What can we say about the solution of the following problem? $$Lu=0 \text{ in } \Omega \\ u|_{S_1}=0...- evinda
- Thread
- Boundary
- Replies: 27
- Forum: Differential Equations
-

Equation for the boundary of rays turning to plane waves
Homework Statement I am given the following figure: These are converging rays that appear to be going to a point F convert to a plane wave upon hitting the boundary between n2 and n1, and I am asked to find the equation for the boundary between n1 and n2 that perfectly accomplishes this...- Cocoleia
- Thread
- Boundary Plane Plane waves Ray Rays Refraction Turning Waves
- Replies: 19
- Forum: Introductory Physics Homework Help
-
M
Graduate Boundary Conductance in nanomaterials
Greetings, I hope this is the right place to ask. I have been working with modeling of thermal conductance, G [W/K] of semi-conductor nanowires as a function of temperature. To start, thermal conductivity of a nanowire is modeled using BTE (Boltzmann Transport Equation). Then the conductance...- MSM
- Thread
- Boundary Conductance
- Replies: 1
- Forum: Atomic and Condensed Matter
-
P
High School What is a homogeneous boundary condition?
What is a homogeneous boundary condition? Or, more explicitly, what would make a boundary condition inhomogeneous Many thanks :)- Physgeek64
- Thread
- Boundary Boundary condition Condition Homogeneous
- Replies: 1
- Forum: Other Physics Topics
-
M
Graduate Fluid Boundary Layer Mathy Question
Hi PF! So after scaling Navier-Stokes for a flow over a flat plate we ultimately arrive at ##f f'' + f''' = 0## subject to ##f(0)=0##, ##f'(0)=0##, and ##f'(\infty) = 1## where independent variable is ##\eta##. The source I was reading is trying to reduce this BVP to an IVP. Thus they suggest...- member 428835
- Thread
- Boundary Boundary layer Fluid
- Replies: 2
- Forum: Mechanics
-
Q
Graduate Fluid Boundary layer in presence of a postive heat gradient
I was wondering how a boundary layer would be dissipative of momentum if it was under the influence of a positive heat gradient. I understand that the reason that we don't see the boundary pressure equal the stagnation pressure is that the boundary is dissipative (so excess pressure above...- Quentin_C
- Thread
- Boundary Boundary layer Fluid Fluid dynamics Gradient Heat Thermodynamics
- Replies: 1
- Forum: Thermodynamics
-
A
Boundary Layer Separation in Laminar and Turbulent Flows
When compared to laminar flows, the fluid "sticks" with the solid surface longer in case of turbulent flows. For example, the angle of separation for flow over a circular cylinder is 80 degrees for laminar flows, and 140 degrees for turbulent flows. What is the reason?- Ali Baig
- Thread
- Boundary Boundary layer Fluid dynamics Fluid flow laminar Separation
- Replies: 1
- Forum: Mechanical Engineering
-
W
Undergrad No Boundary Proposal: Overview, Criticisms & Probes
Any good places to go to get a better layman understanding of the no boundary proposal other than Hawking books? Id like to see what criticisms there are of the model, how has it evolved over time and is there any chance for experimental probes of it.- windy miller
- Thread
- Boundary
- Replies: 4
- Forum: Cosmology
-
F
2nd order ODE boundary value constant input-- stuck
Homework Statement Uxx - SU = A ; 0<x<1 Boundary conditions : Ux(0) = 0 U(1) = 0 The Attempt at a Solution I tried to set a new variable W = u + A, I can get rid of the A in the main equation and U(1) becomes = 1. If I set U= C*esqrt(S)x into the equation, its a trivial solution because of...- fahraynk
- Thread
- 2nd order Boundary Constant Input Ode Stuck Value
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
C
Shear stress at boundary of wall = 0
Homework Statement in the formula of shear stress τ = (V)(Q) / It , Q=Ay = first moment of inertia of area, the area can be located above(or bottom) at the point of interest) when the chosen point is at the wall(boundary) , why shear stress = 0? Homework EquationsThe Attempt at a Solution When...- chetzread
- Thread
- Boundary Shear Shear stress Stress Wall
- Replies: 16
- Forum: Engineering and Comp Sci Homework Help
-
T
Undergrad Unconventional Approaches for Boundary Values in Computing Wave Equations
Hi, I was recently following an example shown in this link and just had a couple questions: http://www.scientificpython.net/pyblog/solving-the-2d-wave-equation-and-making-a-video-of-the-solution I believe I understand the steps, but was just not quite understanding the justification. In the...- TheCanadian
- Thread
- Boundary Computing
- Replies: 2
- Forum: Differential Equations
-
G
Undergrad Is the boundary of a star objective or subjective?
What I mean by this question is the following: If, just for example, we define the surface region of a star as that where the matter undergoes a phase transition from plasma to radiation, then that boundary has an objective physical meaning (let's not bother with the fact that the transition is...- Gerinski
- Thread
- Boundary Star
- Replies: 4
- Forum: Astronomy and Astrophysics
-

Mechanical Boundary condition of a Floating Structure
Dear all, I made a cad of floating structure (the frame only), figure attached below. It should be located in the water and moored, so it can't go anywhere. The CFD simulation was done. So I have fluid force on the structure. Now I want to do mechanical analysis of the structure by apply the...- shade rahmawati
- Thread
- Boundary Boundary condition Condition Floating Mechanical Structure
- Replies: 3
- Forum: Mechanical Engineering
-
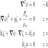
Graduate What are the boundary conditions for rotational flow?
Hello everyone, The boundary condition : P=0, z=ζ is very common when studying irrotational flows. When cast with the Bernoulli equation, it gives rise to the famous dynamic boundary conditionn, which is much more convenient : ∂tφ+½(∇φ)2+gζ=0, z=ζ But what happens if the motion is rotational ...- surfwavesfreak
- Thread
- Bernoulli equation Boundary Boundary condition Condition Fluid mechanics Ocean wave
- Replies: 7
- Forum: Mechanics
-
P
Undergrad Can there be a bounded space w/o a boundary w/o embedding?
Can there be a bounded space without a boundary without embedding in a higher spatial dimension? This seems to be the kind of question I get stuck on when the big bang comes up. Thanks- Pjpic
- Thread
- Boundary Bounded Dimension Space
- Replies: 3
- Forum: Differential Geometry
-
H
Why Reynolds Stress vanishes on boundary of closed volume?
The rate of working of the Reynolds Stress can be written as: where ui is the fluctuating velocity and Ūi is the time-averaged velocity. It is stated in the textbook that, if we integrate the above equation over a closed volume V, the divergence term on the left integrates to zero since τRij...- humphreybogart
- Thread
- Boundary Closed Reynolds Stress Turbulence Volume
- Replies: 2
- Forum: Mechanical Engineering
-

Boundary conditions of that beam.
Hi all! I have to calculate the natural frequency of the system. Any idea of boundary conditions of this case? There is beam supported by two springs on the left side.- WORLDOKO
- Thread
- Beam Boundary Boundary conditions Conditions Modal analysis Natural frequency Vibration
- Replies: 1
- Forum: General Engineering
-
M
Undergrad Infinite square well solution - periodic boundary conditions
If we have an infinite square well, I can follow the usual solution in Griffiths but I now want to impose periodic boundary conditions. I have \psi(x) = A\sin(kx) + B\cos(kx) with boundary conditions \psi(x) = \psi(x+L) In the fixed boundary case, we had \psi(0) = 0 which meant B=0 and...- McLaren Rulez
- Thread
- Boundary Boundary condition Boundary conditions Conditions Infinite Infinite square well Periodic Square Square well
- Replies: 15
- Forum: Quantum Physics
-

MHB Boundary Value Problem: Does it Have a Solution?
Hello! (Wave) I want to check if the following boundary value problem has a solution $\left\{\begin{matrix} -u_{xx}-4u=\sin {2x}, x \in (0,\pi)\\ u(0)=u(\pi)=0 \end{matrix}\right.$ I have thought the following: We consider the corresponding homogeneous equation $-u_{xx}-4u=0$. The...- evinda
- Thread
- Boundary Boundary value problem Value
- Replies: 4
- Forum: Differential Equations
-
P
Undergrad How do the concepts of "boundary"and"infinitesimal" interact
How can something have a definitive edge if space can always be more granular?- Pjpic
- Thread
- Boundary Concepts Granular
- Replies: 5
- Forum: Beyond the Standard Models
-
Graduate Neumann boundary conditions in calculus of variations
In calculus of variations, extremizing functionals is usually done with Dirichlet boundary conditions. But how will the calculations go on if Neumann boundary conditions are given? Can someone give a reference where this is discussed thoroughly? I searched but found nothing! Thanks- ShayanJ
- Thread
- Boundary Boundary conditions Calculus Calculus of variations Conditions Neumann
- Replies: 8
- Forum: Other Physics Topics
-
M
Graduate Solving a Boundary Value Problem: Proving u(x) < 0
I have a BVP of the form u" + f(x)u = g(x) , u(0)=u(1)= 0 where f(x) and g(x) are positive functions. I suspect that u(x) < 0 in the domain 0 < x < 1. How do I go proving this. I have try proving by contradiction. Assuming first u > 0 but I can't deduce that u" > 0 which contradict that u has...- matematikawan
- Thread
- Boundary Boundary value problem Value
- Replies: 7
- Forum: Differential Equations
-

Reflection and Transmission of Plane Waves at a Dielectric-Metal Boundary
Homework Statement Sorry for the dull question. Problem is as shown/attached Homework Equations The waves in part ii) are traveling in a HIL dielectric of permittivity ##\epsilon_{r}## from ##0 <z<d## and then hit an ideal metal boundary at ##z=d##. The Attempt at a Solution I figure this...- bananabandana
- Thread
- Boundary Dielectric Electromagetism Plane Reflection Wave
- Replies: 1
- Forum: Introductory Physics Homework Help
-
K
Capacitor Charge/Discharge boundary conditions for time
Homework Statement Homework Equations 3. The Attempt at a Solution [/B] I know dV=1/C∫idt and that we integrate the voltage from V to V0. What I don't get are the boundary conditions for t - How do we get what we get in the parenthesis? My closest assumption is that the t/T values refer to the...- kev.thomson96
- Thread
- Boundary Boundary conditions Capacitor Conditions Time
- Replies: 3
- Forum: Engineering and Comp Sci Homework Help
-
R
Graduate Valve closure boundary condition
does anyone know what the boundary condition is for a closing valve using the wave equation pde?- rppearso
- Thread
- Boundary Boundary condition closure Condition Valve
- Replies: 1
- Forum: Differential Equations
-

Undergrad Numerical integration of PDEs: How do you satisfy boundary conditions
Suppose we are solving a diffusion equation. ##\frac{\partial}{\partial t} T = k\frac{\partial^2}{\partial x^2} T## On the domain ##0 < x < L## Subject to the conditions ##T(x,0) = f(x) ## and ##T = 0 ## at the end points. My question is: Suppose we solve this with some integration scheme...- davidbenari
- Thread
- Boundary Boundary conditions Conditions Integration Numerical Numerical integration Pdes
- Replies: 5
- Forum: Differential Equations
-
C
Graduate Q: Scalar Boundary Condition & U(1) Isometry - Lewkowycz & Maldacena
I have a simple question about Lewkowycz and Maldacena's paper http://arxiv.org/abs/1304.4926v2'][/PLAIN] http://arxiv.org/abs/1304.4926v2 In section 2, they consider the scalar field in BTZ background ground and require boundary condition of the scalar field, $\phi \sim e^{i\tau}$ . This...- craigthone
- Thread
- Black hole Boundary Boundary condition Condition Isometry Quantum field theory Scalar
- Replies: 1
- Forum: Special and General Relativity
-

C/C++ C++ matrix boundary condition problems
I have created a matrix with a class called Lattice. The lattice is filled with objects of type 'Dipole' which is created with another class. The problem I am having is with boundary conditions when I look for a neighbour. e.g If i pick a dipole on the top row, I want its 'above' neighbour to be...- rolotomassi
- Thread
- Boundary Boundary condition C++ Condition Matrix
- Replies: 3
- Forum: Programming and Computer Science
-
P
Application of boundary conditions in determining the Green's function
Homework Statement Find the Green's function $G(t,\tau)$ that satisfies $$\frac{\text{d}^2G(t,\tau)}{\text{d}t^2}+\alpha\frac{\text{d}G(t,\tau)}{\text{d}t}=\delta(t-\tau)$$ under the boundary conditions $$G(0,\tau)=0~~~\text{ and }~~~\frac{\text{d}G(t,\tau)}{\text{d}t}=0\big|_{t=0}$$ Then...- pondzo
- Thread
- Application Boundary Boundary conditions Conditions Function Green's function Greens function Ordinary differential equation
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
T
Undergrad How Can Boundary Layer Suction Reduce Flow Separation in Pipe Expansion?
I have a question about the following scenario involving a flow separation issue in a pipe expansion The angle of the expansion is 30* - doubling the diameter from 1D to 2D We can consider this flow fully developed with a Reynolds of 5000+ Associated with this expansion is a head loss... -

Graduate Boundary Value Problem Requiring Quarterwave Symmetry
I can't seem to find an explicit or analytical solution to a boundary value problem and thought I might ask those more knowledgeable on the subject than me. If t is an independent variable and m(t) and n(t) are two dependent variables with the following 8 constraints: a) m' =0 @T=0 and...- TheJfactors
- Thread
- Boundary Boundary value problem Symmetry Value
- Replies: 1
- Forum: Differential Equations
-

Solving Laplace Equations using this boundary conditions?
The equation is Uxx + Uyy = 0 And domain of solution is 0 < x < a, 0 < y < b Boundary conditions: Ux(0,y) = Ux(a,y) = 0 U(x,0) = 1 U(x,b) = 2 What I've done is that I did separation of variables: U(x,y)=X(x)Y(y) Plugging into the equation gives: X''Y + XY'' = 0 Rearranging: X''/X = -Y''/Y = k...- astrodeva
- Thread
- Boundary Boundary conditions Conditions Laplace Pde
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Graduate Temperature gradient vs thermal boundary layer thickness
what does the relation between the temperature gradient inside the thermal boundary and thermal boundary layer thickness i mean what will be the temperature gradient ( high or low) when the thermal boundary layer is thick relative to the thin one? Kindly explain mathematically and physically as...- Idrees Afridi
- Thread
- Boundary Boundary layer Gradient Temperature Temperature gradient Thermal Thickness
- Replies: 8
- Forum: Thermodynamics
-
K
Undergrad Sturm-Liouville Problem, boundary condition
given the generalized SL conditions Let's say psi_m and psi_n are eigenfunctions of the given y. Its Wronskian is 0 because otherwise the boundary condition doesn't make sense much. However, I wonder if it is possible to have, S={ x | W[psi_m(x) , psi_n(x)] =/= 0 } otherwise...- kidsasd987
- Thread
- Boundary Boundary condition Condition
- Replies: 1
- Forum: Differential Equations
-

Boundary layer thickness confusion
Hi, PF! Recently, while reading chapter 6 of Incropera's Fundamentals of Heat and Mass Transfer I got into a confusion regarding the velocity boundary layer. The book first states that, as the flow becomes more turbulent, the boundary layer gets thicker, as indicated by both figures attached at...- MexChemE
- Thread
- Boundary Boundary layer Confusion Fluid dynamics Reynolds number Thickness Transport phenomena
- Replies: 7
- Forum: Mechanical Engineering
-
C
Blasius Solution for Boundary Layer
Is the Blasius solution valid for internal flow in an underdeveloped pipe? Can the function for the boundary layer thickness be used to calculate when the boundary layers will meet in the center of the pipe? I don't see how it could be valid since the assumption in its derivation is that...- ccrook
- Thread
- Boundary Boundary layer Flow Fluid mechanics
- Replies: 1
- Forum: Mechanical Engineering
-
A
Graduate Boundary conditions electrostatic potential
I'm modelling a system with a nanosized semiconductor in 1d, inside which I want to find the electrostatic potential. Having found this I am unsure what boundary conditions to put on this, when it is connected to a metal on one side and to vacuum on the other. So far I have put that it is...- aaaa202
- Thread
- Boundary Boundary conditions Conditions Electrostatic Electrostatic potential Potential
- Replies: 3
- Forum: Electromagnetism
-
A
Solving boundary conditions for vibrating beam
Hi there, I'm solving the equation for the transverse vibrations of a Euler-Bernoulli beam fixed at both ends and subject to axial loading. It's a similar problem to that described by Rao on page 355 of his book "Vibration of Continuous Systems" (Google books link), except the example he uses...- ajtgraves
- Thread
- Beam Beams Boundary Boundary conditions Conditions Partial differential equations Vibration
- Replies: 1
- Forum: Engineering and Comp Sci Homework Help
-
A
Graduate Varying The Gibbons-Hawking Term
The Gibbons Hawking boundary term is given as ##S_{GHY} = -\frac{1}{8 \pi G} \int_{\partial M} d^dx \sqrt{-\gamma} \Theta##. I want to calculate its variation with respect to the induced boundary metric, ##h_{\mu \nu}##. The answer (given in eqns 6&7 of...- adsquestion
- Thread
- Boundary Curvature tensor Metric tensor Term
- Replies: 1
- Forum: Special and General Relativity
-
High School What happens at the boundary with light refraction?
There is something I have been wondering about with refraction. There have been many explanations of why the light bends. However, it still does not feel intuitive. The question I have is with how light enters the clear object. Is it proven that light indeed enters at an angle that is instantly... -

Graduate Electromagnetic gauge invariance with boundary conditions
Hello. I'm trying to wrap my head around how Lagrangians work in classical field theory. I have a book that is talking about the gauge invariance of the Lagrangian: \mathscr{L} = -\frac{1}{4}F_{\mu\nu}F^{\mu\nu}-J^\mu A_\mu. It shows that we can replace A^\mu with A^\mu+\partial^\mu\chi for...- Xezlec
- Thread
- Boundary Boundary conditions Conditions Electromagnetic Gauge Gauge invariance Invariance
- Replies: 8
- Forum: Electromagnetism
-
K
Graduate [Electromagnetics] Dielectric boundary condition
http://local.eleceng.uct.ac.za/courses/EEE3055F/lecture_notes/2011_old/eee3055f_Ch4_2up.pdf (Page 4.4 )I am having a trouble with understanding why closed loop line integration is 0 at dielectric boundary. As far as I know, closed loop line integration is 0 because electric field is...- kidsasd987
- Thread
- Boundary Boundary condition Condition Dielectric Electromagnetics
- Replies: 1
- Forum: Electromagnetism
-
T
Graduate Solving a PDE w/ given boundary and initial conditions
Firstly, my main question boils down to speaking about the initial conditions and boundary conditions. I was given: $$ u(0,y,t) = u(\pi,y,t) = u(x,0,t) = u(x,\pi,t) = 0 $$ but then the initial condition was: $$ u(x,y,0) = 1 $$ Aren't the initial and boundary conditions inconsistent in such...- TheCanadian
- Thread
- Boundary Conditions Initial Initial conditions Pde
- Replies: 5
- Forum: Differential Equations
-
M
Graduate Calculus of variations with circular boundary conditions
The Euler-Lagrange equations give a necessary condition for the action be extremal given some lagrangian which depends on some function to be varied over. The basic form assumes fixed endpoints for the function to be varied over, but we can extend to cases in which one or both endpoints are free... -
C
Graduate Boundary layer at airfoil stagnation points
I was reading this: http://www.creatis.insa-lyon.fr/~dsarrut/bib/Archive/others/phys/www.mas.ncl.ac.uk/%257Esbrooks/book/nish.mit.edu/2006/Textbook/Nodes/chap06/node29.html Under the first figure it states "Figure 6.20: The boundary layer at a stagnation point on an airfoil has a constant...- charlies1902
- Thread
- Airfoil Boundary Boundary layer Points Stagnation
- Replies: 1
- Forum: Mechanics
-
S
Boundary conditions shooting method
I am trying to solve the differential equation ##\frac{d^{2}y}{dr^2}+(\frac{1}{r}+1)y=0## with the boundary conditions ##y(r) \rightarrow r \frac{dy}{dr}(0)## as ##r \rightarrow 0## and ##y(r) \rightarrow \sin(kr+\delta)## as ##r \rightarrow \infty##. I know that the shooting method is the...- spaghetti3451
- Thread
- Boundary Boundary conditions Conditions Method Shooting method
- Replies: 1
- Forum: Programming and Computer Science
-
G
Graduate Solving Boundary Conditions in 2D Axisymmetrical Model
Hi! I can't understand how to implement boundary conditions in a 2D axisymmetrical model. How should be the value of pressure, x-velocity and y-velocity at the axis of symmetry? Thank you!- Giorgia
- Thread
- Boundary Boundary conditions Conditions
- Replies: 1
- Forum: Differential Equations