What is Invariant: Definition and 405 Discussions

Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties, such as vector spaces, from the point of view of their effect on functions. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are invariant, under the transformations from a given linear group. For example, if we consider the action of the special linear group SLn on the space of n by n matrices by left multiplication, then the determinant is an invariant of this action because the determinant of A X equals the determinant of X, when A is in SLn.

View More On Wikipedia.org
Recent contents Top users
  1. I

    Spacetime Invariant interval and gamma

    I am revisiting the invariant interval spacetime issue , as explained in the book Spacetime Physics by E.F. Taylor and A. Wheeler. The explanation is clear and the invariant interval is correct, based on the data given and this is the whole point I am making, as explained below. In a...
  2. Ramtin123

    A Why Is the Mixed SU(2) Term Invariant in Scalar Multiplet Models?

    Consider two arbitrary scalar multiplets ##\Phi## and ##\Psi## invariant under ##SU(2)\times U(1)##. When writing the potential for this model, in addition to the usual terms like ##\Phi^\dagger \Phi + (\Phi^\dagger \Phi)^2##, I often see in the literature, less usual terms like: $$\Phi^\dagger...
  3. J

    Massless theories can be conformally invariant

    Homework Statement The exercise needs us to first show that ##P^2## (with ##P_\mu=i\partial_\mu##) is not a Casimir invariant of the Conformal group. From this, it wants us to deduce that only massless theories could be conformally invariant. Homework Equations The Attempt at a Solution I...
  4. G

    I Is energy-momentum invariant and/or conserved?

    Hi. I'm reading an introductory text that somehow seems to confuse if ##E^2-(cp)^2=const## means that the left side is invariant (under Lorentz transformations) or conserved (doesn't change in time). As far as I understand it, they only prove Lorentz invariance. Are they both true? If so...
  5. snoopies622

    B Lorentz Invariant Paths in Spacetime

    Last night I was pleasantly surprised to discover that, given a particle trajectory x^2 - c^2t^2 = a^2 when viewed through a Lorentz transformation x' = \gamma (x-vt) t' = \gamma (t - vx/c^2) produces exactly the same shape x'^2 - c^2t'^2 = a^2 . I suppose this is equivalent to the...
  6. gasar8

    A Lorentz Invariant Phase Space: Symplectic Geometry

    I have an assignment to show that specific intensity over frequency cubed \frac{I}{\nu^3}, is Lorentz invariant and one of the main topics there is to show that the phase space is Lorentz invariant. I did it by following J. Goodman paper, but my professor wants me to show this in another way...
  7. J

    A Hardy's Paradox and lorentz invariant realist interpretation

    Does Hardy's paradox show that all realist interpretations cannot be made lorentz invariant? Or is it just realist hidden variable theories?
  8. N

    A Study Chern-Simons Invariant: Understanding 3-Manifold Measurement

    I've been studying the Witten-Reshetikhin-Turaev (WRT) invariant of 3-manifolds but have almost zero background in physics. The WRT of a 3-manifold is closely related to the Chern-Simons (CS) invariant via the volume conjecture. My question is, what does the CS invariant of a 3-manifold...
  9. J

    A Are Modal interpretations emprically Lorentz invariant?

    Modal interpretations are a class of realist non local hidden variable theories. However, they cannot be made fundamentally lorentz invariant. However, neither can bohmian mechanics but BH is still emprically lorentz invariant. So are modal interpretation empirically lorentz invariant as well?
  10. tworitdash

    B Confirmation of c as Invariant Speed in Our Universe?

    Thank you everyone so much for all the explanations. However, I have another question here. I was reading Mr Tompkins and I understand that relativity of time exists because we have a certain absolute speed, beyond which nothing can travel. For our universe it is c. Are there any other proofs...
  11. Mr Davis 97

    Having all subgroups normal is isomorphism invariant

    Homework Statement A group is called Hamiltonian if every subgroup of the group is a normal subgroup. Prove that being Hamiltonian is an isomorphism invariant. Homework EquationsThe Attempt at a Solution Let ##f## be an isomorphism from ##G## to ##H## and let ##N \le H##. First we prove two...
  12. L

    I A question about invariant mass

    A question of invariable mass. In a inertial system, the invariable mass of a system never change with time. This system may not be an isolated system. Whether in any inertial system, the invariant mass of the system remains unchanged.Or, in a certain inertial system, what is the necessary and...
  13. I

    I Invariant mass plots for resonance 'particles'

    The interaction p + π- → n + π- + π + may proceed by the creation of an intermediate 'particle' or resonance called a rho. This can be detected as a peak in the plot of invariant rest mass energy of the emergent pions versus frequency of pions observed. My question is quite simply, invariant...
  14. Viraj Daniel Dsouza

    I Prove that TDSE is invariant under Galilean Transformation.

    I want the proof for a general wavefunction Ψ(x,t).
  15. N

    Left invariant vector field under a gauge transformation

    Homework Statement For a left invariant vector field γ(t) = exp(tv). For a gauge transformation t -> t(xμ). Intuitively, what happens to the LIVF in the latter case? Is it just displaced to a different point in spacetime or something else? Homework EquationsThe Attempt at a Solution
  16. N

    A Reshetikhin-Turaev Invariant of Manifolds

    The Reshetikhin-Turavev construction comes with an invariant that is sometimes called the Reshetikhin-Turaev Invariant. I'm currently attempting to wrap my head around this construction but was hoping for a sneak peak to help motivate me. My question is, what does the Reshetikhin-Turaev...
  17. N

    I Computation of the left invariant vector field for SO(3)

    I am trying to improve my understanding of Lie groups and the operations of left multiplication and pushforward. I have been looking at these notes: https://math.stackexchange.com/questions/2527648/left-invariant-vector-fields-example...
  18. H

    I Uncovering Invariance in SR: Why is $0 = (cdt)^{2}-dx^{2}$ Invariant?

    In SR why is the following length-interval invariant (1) $$ 0 = (cdt)^{2}-dx^{2}$$ While, (2) $$ 0 = (cdt)^{2}+dx^{2} $$ is not invariant? The first expressions (1) measures the coordinates of a wavefront propagating away from the observer with the speed och light, and since c is a...
  19. P

    How do you show |r_1-r_2| is rotationally invariant

    Homework Statement How do you show |r_1-r_2| is rotationally invariant Homework EquationsThe Attempt at a Solution So i get that we need to show that it is invariant under the transformations ## r_1 \rightarrow r_1 + \epsilon (n \times r_1)## ## r_2 \rightarrow r_2 + \epsilon (n \times r_2)##...
  20. P

    Generating Function for Lagrangian Invariant System

    Homework Statement Given a system with a Lagrangian ##L(q,\dot{q})## and Hamiltonian ##H=H(q,p)## and that the Lagrangian is invariant under the transformation ##q \rightarrow q+ K(q) ## find the generating function, G. Homework EquationsThe Attempt at a Solution ##\delta q = \{ q,G \} =...
  21. BookWei

    I Examples of invariant quantities

    In SR, we know that ##\vec E \cdot \vec B## and ##E^{2}-B^{2}## are invariant. Although I can prove those two invariant physical quantities mathematically, I do not know how to find at least one example to demonstrate that ##\vec E \cdot \vec B## and ##E^{2}-B^{2}## are invariant. Many thanks!
  22. S

    Invariant mass problem, elastic collision

    fHomework Statement Question b: Homework Equations E2=c2p2+m2c4 The Attempt at a Solution We have c2pinitial2=E02-m2c4, and Ef2=c2p2+m2c4 for each outgoing proton. Combining those equations we get c2p2=Ef2-E02+c2pinitial2. I don't know where to go from here.
  23. V

    I Proving Effects of Stress-Energy Tensor on Curvature

    Hi everyone. Could you help me to find the way to prove some things? 1)Changing of body velocity or reference frame don't contribute to spacetime curvature 2)On the contrary the change of body mass causes the change of curvature in local spacetime I use the assumption that if we have the same...
  24. Amaterasu21

    I Getting Invariant Curvature from Momentum & Energy

    Hi all, I understand the mathematics behind special relativity pretty well, but I only have a bare conceptual understanding of general relativity. My understanding is that energy, momentum and stress (as described in the energy-stress tensor) are what contribute to space-time curvature and...
  25. Kara386

    Why is it obvious that this Lagrangian is Lorentz invariant?

    We've just been introduced to Langrangians, and my lecturer has told us that the Lagrangian density ##\mathcal{L} = \frac{1}{2} (\partial ^{\mu}) (\partial_{\mu}) -\frac{1}{2} m^2\phi^2## is obviously Lorentz invariant. Why? Yes it's a scalar, but I can't see why it obviously has to be a Lorentz...
  26. T

    I Invariant element integrand

    Let ##k## be a Lorentz four-vector. The integrand ##d^4k## is the same as ##d^3 k \ dk_0##. Why is this true? ##k_0## is the first component of ##k##. So how are we allowed for equating the two integrands? Just to add context, this situation happens during the construction of the integral for...
  27. B

    I Gravity Invariant with Motion? Exploring Examples

    In simple examples of throwing a ball upward and observing it's arc, the calculations include a constant vector acting downward on the ball throughout it's flight. Without getting into the complications of that vector changing magnitude with altitude, it does not change with respect to the speed...
  28. B

    Dual spinor and gamma matrices

    Here it is a simple problem which is giving me an headache,Recall from class that in order to build an invariant out of spinors we had to introduce a somewhat unexpected form for the dual spinor, i.e. ߰ψ = ψ†⋅γ0 Then showing that ߰ is invariant depends on the result that (ei/4⋅σμν⋅ωμν)† ⋅γ0 =...
  29. binbagsss

    Show that d^4k is Lorentz invariant

    Homework Statement Show that ##d^4k## is Lorentz Invariant Homework Equations [/B] Under a lorentz transformation the vector ##k^u## transforms as ##k'^u=\Lambda^u_v k^v## where ##\Lambda^u_v## satisfies ##\eta_{uv}\Lambda^{u}_{p}\Lambda^v_{o}=\eta_{po}## , ##\eta_{uv}## (2) the Minkowski...
  30. N

    I D meson decay and invariant mass

    Considering a D0->π+K- where the D meson decays from rest. If one was to want to calculate the invariant mass of the D meson by measuring the momenta of the pion and kaon, following from conservation of momentum: m2=(Eπ+EK)2-(pπ+pK)2 However by inputting numerical data Eπ=137MeV EK=493MeV...
  31. moriheru

    I Is a game situation in chess topologically invariant?

    The thought just struck my mind, while I was reading "The art and craft of problem solving", whether a game of chess can be topologically defended and is topologically invariant. For example a game play where only the pawn has been moved to E3 is some sort of topological figure and the initial...
  32. C

    I Scale invariant thermal fluctuations

    There's something that has been bugging me for over a year now and I seem to be unable to find the answer. I would appreciate it very much if somebody could help me out. The thing is that I don't understand how it is possible that in second order phase transitions the correlation legth becomes...
  33. M

    I Constructing left invariant vector fields on SO(3)

    hello every one can one please construct for me left invariant vector field of so(3) rotational algebra using Euler angles ( coordinates ) by using the push-forward of left invariant vector field ? iv'e been searching for a method for over a month , but i did not find any well defined method...
  34. M

    I Lie groups left invariant vector fields

    hello every one . can someone please find the left invariant vector fields or the generator of SO(2) using Dr. Frederic P. Schuller method ( push-forward,composition of maps and other stuff) Dr Frederic found the left invariant vector fields of SL(2,C) and then translated them to the identity...
  35. hilbert2

    A Scale invariant inverse square potential

    Yesterday, I was thinking about a problem I had encountered many years before, the central force problem with a ##V(r) \propto r^{-2}## potential... If we have a Hamiltonian operator ##H = -\frac{\hbar^2}{2m}\nabla^2 - \frac{A}{r^2}## and do a coordinate transformation ##\mathbf{r}...
  36. T

    I How is Graphene's Hamiltonian rotationally invariant?

    Graphene's Hamiltonian contains first order derivatives (from the momentum operators) which aren't invariant under simple spatial rotations. So it initially appears to me that it isn't invariant under rotation. From reading around I see that we also have to perform a rotation on the Pauli...
  37. Demystifier

    I Error in Lorentz Invariant Integration

    Let ##j^{\mu}(x)## be a Lorentz 4-vector field in Minkowski spacetime and let ##\Sigma## be a 3-dimensional spacelike hypersurface with constant time of some Lorentz frame. From those I can construct the quantity $$Q=\int_{\Sigma} dS_{\mu}j^{\mu}$$ where $$dS_{\mu}=d^3x n_{\mu}$$ and ##n_{\mu}##...
  38. L

    Why is Newton's equation of motion invariant to time reversal

    Is there any deep reason behind this? per example the principle of least action or something else?
  39. M

    Show curvature of circle converges to curvature of curve @ 0

    Homework Statement Let γ : I → ℝ2 be a smooth regular planar curve and assume 0 ∈ I. Take t ≠ 0 in I such that also −t ∈ I and consider the unique circle C(t) (which could also be a line) containing the 3 points γ(0), γ(−t), γ(t). Show that the curvature of C(t) converges to the curvature κ(0)...
  40. M

    Invariance of length of curve under Euclidean Motion

    Homework Statement Show that the length of a curve γ in ℝn is invariant under euclidean motions. I.e., show that L[Aγ] = L[γ] for Ax = Rx + a Homework Equations The length of a curve is given by the arc-length formula: s(t) = ∫γ'(t)dt from t0 to tThe Attempt at a Solution I would imagine I...
  41. A

    I Is the mass defect still considered with invariant mass?

    Hello. Suppose you were to assemble a sphere of negative charges. When you are done, the rest mass of the sphere is larger than that of the negative charges because they gain energy in forming the sphere. But the invariant mass of the electrons can't change and apparently gaining energy doesn't...
  42. Luca_Mantani

    A Invariant combination of SU(3) states

    Hi everyone, this is something i know because i saw it many times, but i have never fully understand it. Suppose i have a quark field (singlet under SU(2) let's say) ##q## and i would like to build an invariant term to write in the Lagrangian. The obvious choice is to write a mass-term...
  43. J

    A How is the invariant speed of light enocded in SL(2,C)?

    In quantum field theory, we use the universal cover of the Lorentz group SL(2,C) instead of SO(3,1). (The reason for this is, of course, that representations of SO(3,1) aren't able to describe spin 1/2 particles.) How is the invariant speed of light enocded in SL(2,C)? This curious fact of...
  44. F

    A Metric on ℝ^2 Invariant under Matrix Transformations

    Hello, I am looking for some nontrivial metric on ℝ^2 invariant under the coordinate transformations defined by the 2x2 matrix [1 a12(θ)] [a21(θ) 1], where aik is some real function of θ. In the same way that the Minkowski metric on ℝ^2 is invariant under Lorentz transformations. Does...
  45. S

    Tresca criterion in terms of invariants

    Hi, The Tresca Critrion is given in the form of non continuous equations: Max(½|σ1-σ2|,½|σ2-σ3|,½|σ3-σ1|) = k How did they come up with the invarient equation f(J2,θ) = 2√J2 * sin(θ+⅓π)-2k, θ from (0 to 60)
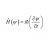
  46. Vitor Pimenta

    Sublimation: invariant heat or internal energy?

    Homework Statement Below, two experiments (1 and 2) are described, in which the same quantity of solid carbon dioxide is completely sublimated, at 25ºC: The process is carried out in a hermetically sealed container, non-deformable with rigid walls; The process is carried out in a cilinder...
  47. J

    I On the invariant speed of light being the upper speed limit

    Hello! I have a question that has been bothering me since I first started learning about Special Relativity: Given only the Minskowskian metric and/OR the spacetime interval, how can one reach the conclusion that the speed of light is invariant for every observer and how can one conclude that it...
  48. V

    Galilean and Lorentz invariant

    Homework Statement Professor C. Rank claims that a charge at (r_1, t_1) will contribute to the air pressure at (r_2, t_2) by an amount B \sin[C(|r_2 − r_1|^2− c^2|t_2 − t_1|^2)] , where B and C are constants. (A) Is this effect Galilean invariant? (B) Is this effect Lorentz invariant...
  49. F

    B Is Energy Galilean Invariant?

    As the title says, is energy Galilean invariant? I'm fairly sure it isn't, since if one considers the simple case of a free particle, such that its energy is ##E=\frac{p^{2}}{2m}##, then under a Galilean boost, it follows that ##E'=...
  50. nmsurobert

    Calculating Invariant Mass in LHC Collisions: A Proton Beam Energy Question

    Homework Statement At the LHC at CERN protons with an energy of 6.5 TeV (= 6.5·1012eV) each are collided with each other.To achieve the same invariant mass in a fixed target experiment, what would the energy of the proton beam have to be? Homework Equations E2 - p2c2 = m2c4 E2 - p2c2=...
Back
Top