Vector space Definition and 530 Threads
-

MHB 307.8.1 Suppose Y_1 and Y_2 form a basis for a 2-dimensional vector space V
nmh{796} $\textsf{Suppose $Y_1$ and $Y_2$ form a basis for a 2-dimensional vector space $V$ .}\\$ $\textsf{Show that the vectors $Y_1+Y_2$ and $Y_1−Y_2$ are also a basis for $V$.}$ $$Y_1=\begin{bmatrix}a\\b\end{bmatrix} \textit{ and }Y_2=\begin{bmatrix}c\\d\end{bmatrix}$$ $\textit{ then }$...- karush
- Thread
- Basis Form Space Vector Vector space
- Replies: 8
- Forum: Linear and Abstract Algebra
-

Undergrad Expanding a given vector into another orthonormal basis
Equation 9.2.25 defines the inner product of two vectors in terms of their components in the same basis. In equation 9.2.32, the basis of ## |V \rangle## is not given. ## |1 \rangle ## and ## |2 \rangle ## themselves form basis vectors. Then how can one calculate ## \langle 1| V \rangle ## ? Do...- Pushoam
- Thread
- Basic mathematics Basis Orthonormal basis Shankar Vector Vector space
- Replies: 1
- Forum: Linear and Abstract Algebra
-

Checking the linear independence of elements of 2 X 2 matrices
Homework Statement Homework Equations 3. The Attempt at a Solution [/B] ## |3 \rangle = |1 \rangle - 2 ~ |2 \rangle ## So, they are not linearly independent. One way to find the coefficients is : ## |3 \rangle = a~ |1 \rangle +b~ |2 \rangle ## ...(1) And solve (1) to get the values of a...- Pushoam
- Thread
- Elements Exercise Independence Linear Linear independence Matrices Vector space
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-

Functions forming a vector space
Homework Statement 1.1.3 1) Do functions that vanish at the endpoints x=0 and L=0 form a vector space? 2) How about periodic functions? obeying f(0)=f(L) ? 3) How about functions that obey f(0)=4 ? If the functions do not qualify, list what go wrong.Homework Equations The Attempt at a...- Pushoam
- Thread
- Exercise Functions Space Vector Vector space
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-

Show: Vectors e.g.(a,b,1) do not form vector space.
Homework Statement Homework Equations definition of null vector, [/B] The Attempt at a Solution null vector : ## |0 \rangle = (0,0,0) ## inverse of (a,b,c) = ( - a, -b, -c) vector sum of the two vectors of the same form e.g. (c,d,1) + ( e,f,1) = ( c+e, d+f, 2) does not have the same...- Pushoam
- Thread
- Form Shankar Space Vector Vector space Vectors
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
I
Determining if a subset W is a subspace of vector space V
Homework Statement Let V = RR be the vector space of the pointwise functions from R to R. Determine whether or not the following subsets W contained in V are subspaces of V. Homework Equations W = {f ∈ V : f(1) = 1} W = {f ∈ V: f(1) = 0} W = {f ∈ V : ∃f ''(0)} W = {f ∈ V: ∃f ''(x) ∀x ∈ R} The...- iJake
- Thread
- Linear algebra Space Subspace Subspaces Vector Vector space Vector spaces
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
S
Undergrad Understanding Z2 Graded Vector Spaces: Definition and Examples
Hello! I just started reading about ##Z_2## graded vector spaces (and graded vector spaces in general) and I want to make sure I understand from the beginning. So the definition, as I understand it, is that a graded vector space can be decomposed into subspaces of degree 0 and 1. So ##V=V_1...- Silviu
- Thread
- Space Vector Vector space
- Replies: 3
- Forum: Linear and Abstract Algebra
-

[Linear Algebra] Show that H ∩ K is a subspace of V
Homework Statement From Linear Algebra and Its Applications, 5th Edition, David Lay Chapter 4, Section 1, Question 32 Let H and K be subspaces of a vector space V. The intersection of H and K is the set of v in V that belong to both H and K. Show that H ∩ K is a subspace of V. (See figure.)...- bornofflame
- Thread
- Algebra Intersection Linear algebra Subspace Union Vector space
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
K
Undergrad Expressing Locality in Vector Space for GR
How do we express the locality of a vector space in general relativity? I mean, it's not clear what the boundaries of a given vector space are. To put in another way, we could, in principle, blindly consider that we have the entire of ##\mathbb{R}^4## at our disposal to describe, say, the...- kent davidge
- Thread
- Locality Space Vector Vector space
- Replies: 4
- Forum: Special and General Relativity
-

Determine if function forms a vector space
Homework Statement Problem- Determine if the set of all function y(t) which have period 2pi forms a vector space under operations of function addition and multiplication of a function by a constant. What I know- So I know this involves sin, cos, sec, and csc. Also I know that a vector space...- Carson
- Thread
- Forms Function Linear algebra Space Vector Vector space
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

High School Why is it Important that something is a vector space?
hi I am studying algebra and i have a question. why is important that something is a vector space?, i mean, what implications have? matrix, complex numbers , functions , n-tuples. What do these have in common, apart from being a vector space? why is so important that a certain set of...- MAGNIBORO
- Thread
- Important Space Vector Vector space
- Replies: 10
- Forum: Linear and Abstract Algebra
-
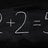
Is the zero Matrix a vector space?
Homework Statement So I have these two Matrices: M = \begin{pmatrix} a & -a-b \\ 0 & a \\ \end{pmatrix} and N = \begin{pmatrix} c & 0 \\ d & -c \\ \end{pmatrix} Where a,b,c,d ∈ ℝ Find a base for M, N, M +N and M ∩ N. Homework Equations I know the 8 axioms about the vector spaces. The...- Alex Langevub
- Thread
- Bases Matrices Matrix Space Vector Vector space Vector spaces Zero
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

MHB What is the basis of the trivial vector space {0}
It makes me wonder... wikipedia says about a basis: [FONT=Times New Roman]In mathematics, a set of elements (vectors) in a vector space V is called a basis, or a set of basis vectors, if the vectors are linearly independent and every vector in the vector space is a linear combination of this...- I like Serena
- Thread
- Basis Space Vector Vector space
- Replies: 17
- Forum: Linear and Abstract Algebra
-
R
Undergrad A different way to express the span
Let us assume that d is a vector in the vector space ℝ2 , then is: {td | t ∈ ℝ} the same as span{d} ? Thank you.- Raymondyhq
- Thread
- linear algebra span vector space
- Replies: 8
- Forum: Linear and Abstract Algebra
-
Y
MHB What Is Required to Prove a Subset is a Vector Space?
Hello all, I have a theoretical question regarding subspaces. If V is a subset of a vector space, and we wish to show that V is a vector space itself, we need to show 3 things. Some references say we need to show: a) V is not empty b) V is closed under + c) V is closed under scalar...- Yankel
- Thread
- Space Subspace Vector Vector space
- Replies: 3
- Forum: Linear and Abstract Algebra
-

Undergrad Is Euclidean Space Inherently Geometric or Just a Vector Space?
Or is it something separate that acts on a geometric space? So we know that the Euclidean space is a vector space. But is it geometric? I ask this because in group theory, the group elements are the operators acting on another set, but clearly we see that this doesn't mean that the group...- FallenApple
- Thread
- Geometric Space Vector Vector space
- Replies: 32
- Forum: Linear and Abstract Algebra
-

Solving Vector Spaces Tasks: Basis and Linear Transformations
Hello, everybody! I would really appreciate if someone could help me understand how to solve the following two tasks. I am not sure whether my translation is correct, so if, by any chance, you know a more appropriate terminology, please let me know. I am not fluent in writing matrices here on...- peroAlex
- Thread
- Linear algebra Vector Vector space Vector spaces
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-

Undergrad Difference between an Algebra and a Vector space
Hi guys, I am a little confused on the difference between an Algebra and a vector space. I´m guessing there´s a fairly simple distinction. Any guidance would be much appreciated, I accept both hand wavy and hardcore axiom based responses :) Cheers- Milsomonk
- Thread
- Algebra Difference Space Vector Vector space
- Replies: 2
- Forum: Linear and Abstract Algebra
-
Is it possible that a subspace is not a vector space
<Mentor's note: moved from general mathematics to homework. Thus no template.> Prove subspace is only a subset of vector space but not a vector space itself. Even a subspace follows closed under addition or closed under multiplication,however it is not necessary to follow other 8 axioms in...- tze liu
- Thread
- Space Subspace Vector Vector space
- Replies: 14
- Forum: Precalculus Mathematics Homework Help
-
F
Finding Linearly Independent Vectors in Subspaces
Homework Statement The vectors ##a_1, a_2, a_3, b_1, b_2, b_3## are given below $$\ a_1 = (3~ 2~ 1 ~0) ~~a_2 = (1~ 1~ 0~ 0) ~~ a_3 = (0~ 0~ 1~ 0)~~ b_1 = (3~ 2~ 0~ 2)~~ b_2 = (2 ~2~ 0~ 1)~~ b_3 = (1~ 1~ 0~ 1) $$ The subspace of ## \mathbb R^4 ## spanned by ##a_1, a_2, a_3## is denoted by...- Faiq
- Thread
- Linear Matrices Vector space
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
M
Decomposing space of 2x2 matrices over the reals
Homework Statement Consider the subspace $$W:=\Bigl \{ \begin{bmatrix} a & b \\ b & a \end{bmatrix} : a,b \in \mathbb{R}\Bigr \}$$ of $$\mathbb{M}^2(\mathbb{R}). $$ I have a few questions about how this can be decomposed. 1) Is there a subspace $$V$$ of...- Mathkid3242
- Thread
- Linear algebra Matrices Space Vector space
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Span and Vector Space: Understanding Vectors in Linear Algebra
Homework Statement The question is: if vectors v1, v2, v3 belong to a vector space V does it follow that: span (v1, v2, v3) = V span (v1, v2, v3) is a subset of V.[/B] 2. The attempt at a solution: If I understand it correctly the answer to both questions is yes. The first: the linear...- Poetria
- Thread
- Linear algebra Space Span Vector Vector space
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
J
Complex periodic functions in a vector space
Homework Statement Consider the set V + {all periodic *complex* functions of time t with period 1} Draw two example functions that belong to V. Show that if f(t) and g(t) are members of V then so is f(t) + g(t)Homework EquationsThe Attempt at a Solution f(t) = e(i*w0*t)) g(t) =e(i*w0*t...- jendrix
- Thread
- Complex Functions Periodic Periodic functions Space Vector Vector space
- Replies: 28
- Forum: Calculus and Beyond Homework Help
-
C
Linear Algebra - Finding coordinates of a set
Homework Statement Find the coordinates of each member of set S relative to B. B = {1, cos(x), cos2(x), cos3(x), cos4(x), cos5(x)} S = {1, cos(x), cos(2x), cos(3x), cos(4x), cos(5x)} I am to do this using Mathematica software. Each spanning equation will need to be sampled at six separate...- cscott0001
- Thread
- Algebra Basis vectors Coordinates Linear Linear algebra Set Vector space
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Basis of the intersection of two spaces
Homework Statement Consider two vector spaces ##A=span\{(1,1,0),(0,2,0)\}## and ##B=\{(x,y,z)\in\mathbb{R}^3 s.t. x-y=0\}##. Find a basis of ##A\cap B##. I get the solution but I also inferred it without all the calculations. Is my reasoning correct Homework Equations linear dependence...- Zero2Infinity
- Thread
- Basis Basis vectors Intersection Linear algebra Vector space
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Undergrad Existence of spanning set for every vector space
I know that the span of any subset of vectors in a vector space is also a vector space (subspace), but is it true that every vector space has a generating set? That is, the moment that we define a vector space, does there necessarily exist a spanning set consisting of its vectors?- Mr Davis 97
- Thread
- Existence Set Space Vector Vector space
- Replies: 5
- Forum: Linear and Abstract Algebra
-
F
Undergrad Understanding Separable Vector Spaces: The Basics Explained
Dear forum, I am trying to understand what a separable vector space is. I know we can perform the tensor product of two or more vector space and obtain a new vector space. Is that vector space separable because it is the product of other vector spaces? thanks- fog37
- Thread
- Separable Space Vector Vector space
- Replies: 9
- Forum: Linear and Abstract Algebra
-
M
MHB Is $\Phi|_{U_2}$ a Vector Space Isomorphism?
Hey! :o Let $V$ be the real vector space $\mathbb{R}[X]$ and $M \subset \mathbb{R}$ a set with $d$ elements. Let $$U_1 := \{ f \in \mathbb{R}[X] | \forall m \in M : f(m) = 0\}, \ \ U_2 := \{ f \in \mathbb{R}[X] \mid \deg(f) \leq d − 1\}$$ be two vector spaces of $V$. Let $\Phi: V\rightarrow...- mathmari
- Thread
- Isomorphism Space Vector Vector space
- Replies: 1
- Forum: Linear and Abstract Algebra
-
F
Undergrad Basis of a Subspace of a Vector Space
Hello Forum and happy new year, Aside from a rigorous definitions, a linear vector space contains an infinity of elements called vectors that must obey certain rules. Based on the dimension ##N## (finite or infinite) of the vector space, we can always find a set of ##n=N## linearly independent...- fog37
- Thread
- Basis Space Subspace Vector Vector space
- Replies: 8
- Forum: Linear and Abstract Algebra
-
L
MHB Solve Vector Space Question: Get the Solution Now
How do you solve this question I just need a solution- LearnerJr
- Thread
- Space Vector Vector space
- Replies: 3
- Forum: Linear and Abstract Algebra
-
A
Undergrad Understanding Spinors - Geometry & Usage
Okay, I have read on spinors here and there but I really don't understand geometrically or intuitively what it is. Can someone please explain it to me and how/when it is used? Thanks!- Aakash Lakshmanan
- Thread
- Geometry Spinor Vector space
- Replies: 16
- Forum: Quantum Physics
-
M
Undergrad Is Every Isomorphism in Vector Spaces Reflexive?
Hello all. I have a question about a reflexive relation. Consider ##1_V : V \rightarrow V## with ##V## a vector space. Obviously, this is an isomorphism. My book uses this example to show that V is isomorphic with V (reflexive relationship). However, suppose I have a function ##f: V\rightarrow...- member 587159
- Thread
- Isomorphism Linear algebra Relation Vector space
- Replies: 15
- Forum: Linear and Abstract Algebra
-

Showing that "zero vector space" is a vector space
Homework Statement Let ## \mathbb{V} = \{0 \}## consist of a single vector ##0## and define ##0 + 0 = 0## and ##c0 = 0## for each scalar in ##\mathbb{F}##. Prove that ##\mathbb{V}## is a vector space. Homework EquationsThe Attempt at a Solution Proving that the first six axioms of a vector...- Mr Davis 97
- Thread
- Linear algebra Space Vector Vector space
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
M
Undergrad Proof that every basis has the same cardinality
Hello all. I have a question concerning following proof, Lemma 1. http://planetmath.org/allbasesforavectorspacehavethesamecardinalitySo, we suppose that A and B are finite and then we construct a new basis ##B_1## for V by removing an element. So they choose ##a_1 \in A## and add it to...- member 587159
- Thread
- Basis Cardinality Linear algebra Proof Vector space
- Replies: 2
- Forum: Linear and Abstract Algebra
-
M
Proving Vector Space Property: αa = 0 ⟹ α = 0 or a = 0
Homework Statement Prove that in any vector space V, we have: ##\alpha \overrightarrow a = \overrightarrow 0 \Rightarrow \alpha = 0 \lor \overrightarrow a = \overrightarrow 0## Homework Equations I already proved: ##\alpha \overrightarrow 0 = \overrightarrow 0## ##0 \overrightarrow a =...- member 587159
- Thread
- Linear algebra Property Space Vector Vector space
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
M
Vector space properties: distributivity
Homework Statement I want to proof, using the axioms of a vector space, that: ##(\alpha - \beta)\overrightarrow a = \alpha \overrightarrow a - \beta \overrightarrow a## Homework Equations Definition vector space: The Attempt at a Solution ##(\alpha - \beta)\overrightarrow a = (\alpha +...- member 587159
- Thread
- Properties Space Vector Vector space
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
K
Proving That Any Vector in a Vector Space V Can Be Written as a Linear Combination of a Basis Set
Homework Statement Show that any vector in a vector space V can be written as a linear combination of a basis set for that same space V. Homework Equations http://linear.ups.edu/html/section-VS.html We are suppose to use the 10 rules in the above link, plus the fact that if you have a lineraly...- kregg87
- Thread
- Basis Combination Linear Set Space Vector Vector space
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
G
Distance from a point to a plane
Homework Statement What is the distance from the point P to the plane S? Homework Equations ## S = \left \{ r_{0} + s(u_{1},u_{2},u_{3})+t(v_{1},v_{2},v_{3}) | s,t \in \mathbb{R} \right \} ## The Attempt at a Solution [/B] I found an expression for the general distance between point P and a...- GwtBc
- Thread
- Partial derivative Plane Point Vector space
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
S
Undergrad No problem, it's always good to have multiple sources!
Hello. If I represent a vector space using matrices, for example if a 3x1 vector, V, is represented by 3x3 matrix, A, and if this vector was the eigenvector of another matrix, M, with eigenvalue v, if I apply M to the matrix representation of this vector, does this holds: MA=vA? Also, if I...- Silviu
- Thread
- Eigenvalue Representation Representation theory Vector Vector space
- Replies: 6
- Forum: Linear and Abstract Algebra
-
M
Undergrad Proving Vector Space of Circles is Not Axiomatic
Hi How can i prove that the set if circles does not form a vector space AXIOMATICALLY . ( i am not considering a circle lives in xy-plane ( subset ) as a subspace of xy-plane- mikeeey
- Thread
- Circles Space Vector Vector space
- Replies: 2
- Forum: Linear and Abstract Algebra
-

Undergrad Same vector space for arbitrary independent vectors?
If we use n linearly independent vectors x1,x2...xn to form a vector space V and use another set of n linearly independent vectors y1,y2...yn to form a vector space S, is it necessary that V and S are the same? Why? If we have a vector space Q that the dimension is n, can we say that any set of...- kelvin490
- Thread
- Independent Linear algebra Linear dependence Space Vector Vector algebra Vector space Vectors
- Replies: 4
- Forum: Linear and Abstract Algebra
-
D
Determine if L is a vector space
Homework Statement V = function space from R to R L ={ f in V | f(1/2) > f(2) } Determine if L is a vector space.Homework EquationsThe Attempt at a Solution 1. Closed under addition: Do i do addition like this let g and e in V, then g(1/2)+e(1/2) > g(2) + e(2) but the addiction of two...- Dank2
- Thread
- Space Vector Vector space
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
S
Does V Qualify as a Subspace of ℝ3?
Homework Statement Let X=ℝ3 and let V={(a,b,c) such that a2+b2=c2}. Is V a subspace of X? If so, what dimensions? Homework Equations A vector space V exists over a field F if V is an abelian group under addition, and if for each a ∈ F and v ∈ V, there is an element av ∈ V such that all of...- SYoungblood
- Thread
- Linear algebra Subspace Vector space
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
J
Proving a set of matrices is NOT a vector space
Homework Statement Show that the following is NOT a vector space: {(a, 1) | a, b, c, ∈ ℝ} {(b, c) Note: this is is meant to be a 2x2 matrix. This may not have been clear in how I formatted it. 2. The attempt at a solution I am self-studying linear algebra, and have had a difficulty...- jcw0616
- Thread
- Homework Linear algebra Matrices Set Space Vector Vector space
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
G
Graduate What is the Poynting "vector" mathematically?
Hi. The Poynting vector is a 3-tuple of real or complex numbers (depending on the respective formulation of electrodynamics) times a unit. It may be pictured as an arrow with some length and direction in IR^3 or IC^3. But is it a "vector" in the strict mathematical sense, i.e. an element of a...- greypilgrim
- Thread
- Decoherence Interference Poynting vector Vector Vector space
- Replies: 1
- Forum: Electromagnetism
-
G
Matrix of linear transformation
Homework Statement Let A:\mathbb R_2[x]\rightarrow \mathbb R_2[x] is a linear transformation defined as (A(p))(x)=p'(x+1) where \mathbb R_2[x] is the space of polynomials of the second order. Find all a,b,c\in\mathbb R such that the matrix \begin{bmatrix} a & 1 & 0 \\ b & 0 & 1 \\ c & 0...- gruba
- Thread
- Linear Linear transformation Matrices Matrix Polynomials Transformation Vector space
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
G
Solution set: S = {(8 + 7z, 6 + 5z, z, 1) : z ∈ ℝ}
Homework Statement Plot the solution set of linear equations x-y+2z-t=1 2x-3y-z+t=-1 x+7z=8 and check if the set is a vector space. 2. The attempt at a solution Augmented matrix of the system: \begin{bmatrix} 1 & -1 & 2 & -1 & 1 \\ 2 & -3 & -1 & 1 & -1 \\ 1 & 0 & 7 & 0 & 8 \\...- gruba
- Thread
- Linear Linear algebra Linear system System System of equations Vector space
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-

MHB Dual Vector Space and Dual Basis - another question - Winitzki Section 1-6
I am reading Segei Winitzki's book: Linear Algebra via Exterior Products ... I am currently focused on Section 1.6: Dual (conjugate) vector space ... ... I need help in order to get a clear understanding of an aspect of the notion or concept of the dual basis $$ \{ e^*_1, e^*_2, \ ... \ ...- Math Amateur
- Thread
- Basis Dual Dual basis Section Space Vector Vector space
- Replies: 2
- Forum: Linear and Abstract Algebra
-

High School What Does Dimension Mean in Vector Spaces?
I'm confused about this. I know that if the dimension of the vector space is say, 2, then there will be 2 elements, right? eg. ## \left( \begin{array}{cc} 1 & 0\\ 0 & -1 \end{array} \right)## What I want to know is if the dimension of vector space is still two if the matrix is like this...- toforfiltum
- Thread
- Dimension Space Vector Vector space
- Replies: 6
- Forum: Linear and Abstract Algebra
-
K
How Does the Direct Sum Relate to Unique Decomposition in Vector Spaces?
During lecture, the professor gave us a theorem he wants us to prove on our own before he goes over the theorem in lecture. Theorem: Let ##V_1, V_2, ... V_n## be subspaces of a vector space ##V##. Then the following statements are equivalent. ##W=\sum V_i## is a direct sum. Decomposition of...- Kevin_H
- Thread
- Direct sum Linear algebra Proof Sum Vector Vector space Vector spaces
- Replies: 1
- Forum: Calculus and Beyond Homework Help