Clutch306
- 7
- 0
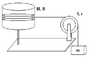
A uniform solid cylinder of mass M = 4.0kg and radius R = 0.40m rotates about a vertical axis on frictionless bearings. A massless cord is wrapped around the cylinder and passes over a pulley of rotational inertia I = 0.020 kg*m2 and radius r = 0.10m. The free end of the cord is attached to a small object of mass m = 1.0kg. There is no friction on the pulley axis and cord does not slip on the pulley.
(a) What is the speed V of the object after it falls a distance h = 1.0m from rest?
(b) What is the angular velocity of the cylinder corresponding to V?
(c) What is the angular velocity of the pulley corresponding to V?
(a) What is the speed V of the object after it falls a distance h = 1.0m from rest?
(b) What is the angular velocity of the cylinder corresponding to V?
(c) What is the angular velocity of the pulley corresponding to V?