Innoko
- 9
- 0
It is told, that all homework-like threads should be posted there. So, here I go.
Imagine such a situation: there is a vertical rod and a cylinder, with the hole diameter sightly larger than the diameter of rod. There is also a second rod, attached to the cylinder perpendicularly. There is a friction between the main rod and the cylinder. It is known, that if we put a cylinder on the rod (watch picture) and apply a force at the edge of the second rod, the system stays rest, i.e. there is lack of rotational and translational motion in it.
On the picture frictional forces are colored with red, normal forces with green.
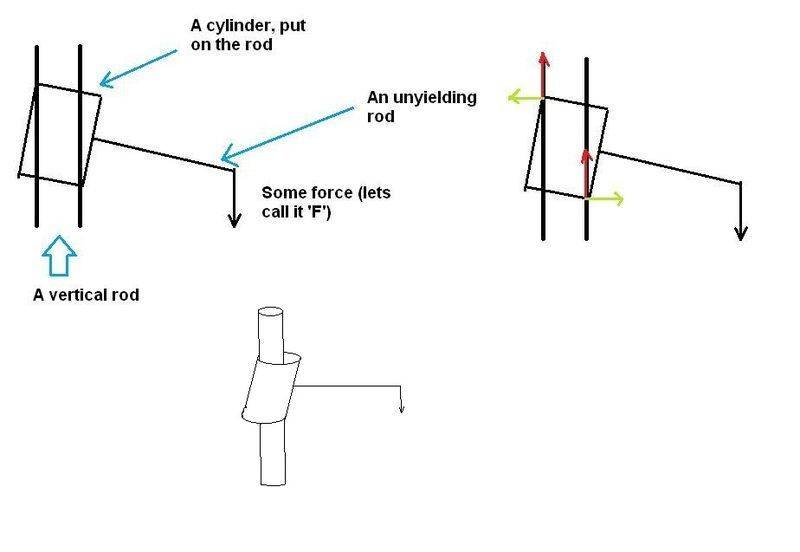
The question is:
-What can we say about frictional forces in the system, if the geometry of the problem is fully known?
-Can we find their quantities, if the mass of the cylinder and the force applied are known?
-Can we answer at least a qualitative question: which one is bigger - applied to the right or to the left corner?
-May they be equal before reaching their maximal quantities (kN, where k is coefficient of friction)?
-Can it be so, that one of them is always reaches it's maximal value and the other doesn't? Under which conditions?
-Can the boundary conditions be founded?
That's clear for me, that we can write down three equitations: protections of the second Newton's law on vertical (here we can fund sum of friction forces) axis, on horizontal axis (here we from here we can clearly understand, that both normal forces are equal!) and the equation, that tells us: the total momentum is equal zero. But this way we get 3 equations with 4 variables (both frictional forces and both normal forces, which are claimed to be equal). Have you got any ideas of how can we find out one more equation?
All bodies are solid.
The force applied is vertical.
PS: it isn't some kind of a homework or other stuff. I just wonder, what is the answer and can't find it myself. You won't find this problem in any book!
PSS: Sorry for my English. Write it down, if you've found some mistakes here, but remember, that it's not the point of the conversation!
Thank you for attention!
Imagine such a situation: there is a vertical rod and a cylinder, with the hole diameter sightly larger than the diameter of rod. There is also a second rod, attached to the cylinder perpendicularly. There is a friction between the main rod and the cylinder. It is known, that if we put a cylinder on the rod (watch picture) and apply a force at the edge of the second rod, the system stays rest, i.e. there is lack of rotational and translational motion in it.
On the picture frictional forces are colored with red, normal forces with green.
The question is:
-What can we say about frictional forces in the system, if the geometry of the problem is fully known?
-Can we find their quantities, if the mass of the cylinder and the force applied are known?
-Can we answer at least a qualitative question: which one is bigger - applied to the right or to the left corner?
-May they be equal before reaching their maximal quantities (kN, where k is coefficient of friction)?
-Can it be so, that one of them is always reaches it's maximal value and the other doesn't? Under which conditions?
-Can the boundary conditions be founded?
That's clear for me, that we can write down three equitations: protections of the second Newton's law on vertical (here we can fund sum of friction forces) axis, on horizontal axis (here we from here we can clearly understand, that both normal forces are equal!) and the equation, that tells us: the total momentum is equal zero. But this way we get 3 equations with 4 variables (both frictional forces and both normal forces, which are claimed to be equal). Have you got any ideas of how can we find out one more equation?
All bodies are solid.
The force applied is vertical.
PS: it isn't some kind of a homework or other stuff. I just wonder, what is the answer and can't find it myself. You won't find this problem in any book!
PSS: Sorry for my English. Write it down, if you've found some mistakes here, but remember, that it's not the point of the conversation!
Thank you for attention!
Last edited: