Calculating Acceleration and Tension in a Pulley System

AI Thread Summary
The discussion focuses on calculating the relationship between the accelerations and tensions in a pulley system involving two masses, m1 and m2, connected through pulleys. It is suggested that the accelerations a1 and a2 of the masses are equal due to their attachment, but clarification is needed on how the floating pulley affects these values. The tension in the strings must also be determined, with considerations for the fixed length of the string connected to m2. Understanding the movement of the pulleys and their impact on the system's dynamics is crucial for solving the problem. The conversation emphasizes the need for a clear visual representation to aid in comprehension.
Warrzie
Messages
3
Reaction score
0
This one has me clueless. The problem reads:

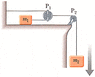
"An object of mass m1 on a frictionless horizontal table is connected to an object of mass m2 through a very light pulley P1 and a light fixed pulley P2."

It wants me to state the relationship between the accelerations, with a1 and a2 corresponding to m1 and m2 respectively.

It then wants the tension in both strings, and finally the acceleration of each block in terms of m1, g, and m2

I've stared at the attached figure for a while and don't even understand how m2's string is connect to the floating pulley, or if that pulley even has an effect on the accelerations/tension. I want to say that a1=a2 since the blocks are attached to each other.

Any hints?
 

Attachments

  • p4-38.gif
    p4-38.gif
    10.3 KB · Views: 566
Physics news on Phys.org
You may want to put a link to the image instead of an attachment, since these usually don't work.
 
I've stared at the attached figure for a while and don't even understand how m2's string is connect to the floating pulley, or if that pulley even has an effect on the accelerations/tension. I want to say that a1=a2 since the blocks are attached to each other.
The acceleration of m2 = acceleration of pulley P1. On has to determine the accleration of m1 and the acceleration of P1. When P1 moves (translates) \Delta{x}, by what distance does m1 translate? One may assume the string tied to m2 is fixed to the axis of P1 and is of fixed length.
 
Last edited:
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Thread 'Electric field due to charges between 2 parallel infinite planes'

TL;DR Summary: Find Electric field due to charges between 2 parallel infinite planes using Gauss law at any point Here's the diagram. We have a uniform p (rho) density of charges between 2 infinite planes in the cartesian coordinates system. I used a cube of thickness a that spans from z=-a/2 to z=a/2 as a Gaussian surface, each side of the cube has area A. I know that the field depends only on z since there is translational invariance in x and y directions because the planes are...
View full post »

Similar threads

Using Effective Mass to find the accelerations of 3 masses connected by pulleys
Replies
25
Views
3K
Newton's Second Law (Pulley Sustem)
Replies
3
Views
2K
Problem with two pulleys and three masses
3
Replies
102
Views
7K
Olympiad dynamics problem with 3 masses and a pulley
Replies
17
Views
2K
Accelerating pulleys (3 pulleys and 3 masses)
Replies
5
Views
2K
Pulley system problem: 6 Pulleys and 1 Mass
Replies
5
Views
913
Acceleration of rising mass and tension in cord
Replies
33
Views
3K
3 pulley problem with attached masses
Replies
15
Views
6K
What if check: Am I calculating tension wrong?
Replies
3
Views
2K
Calculating tensions and acceleration
Replies
10
Views
2K

Hot Threads

Recent Insights

Back
Top