Double Integral problem What am I suppose to do? Related to polar coordinates.

[DavidAp]

The problem and my work is shown in the image below. However, I feel like I did something horrible wrong but I'm not sure where!

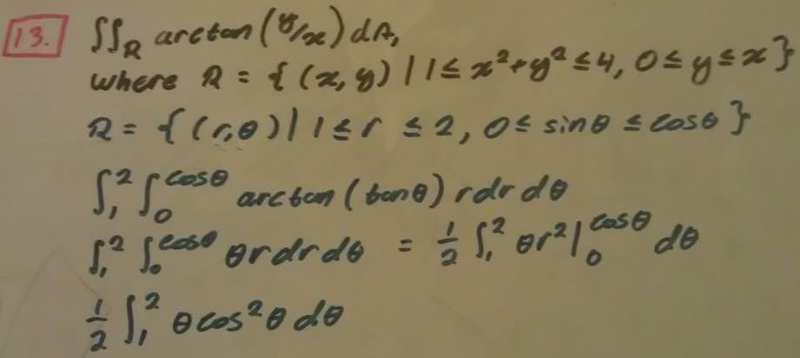
I'm sorry if my handwriting is illegible. If you're having difficulties please leave a comment and I will not hesitate to type it out as a response. Any guidance is greatly appreciated.

Thank you for taking the time to review my question.

 

[Stimpon]

You've got \theta ranging from 0 to cos(\theta), that doesn't make any sense. I'm fairly sure you should have \theta going from 0 to \frac{\pi}{4}. Which you'll be able to see if you draw a picture of R.

 

[DavidAp]

You've got \theta ranging from 0 to cos(\theta), that doesn't make any sense. I'm fairly sure you should have \theta going from 0 to \frac{\pi}{4}. Which you'll be able to see if you draw a picture of R.

I don't know how to draw 0 <= y <= x. I think that might be part of my problem...

I did something wrong though when using pi/2! The answer is 3/64 pi^2 but I keep getting 3/16 pi^2! Why is my denominator 4x less than the answer? Here's my work.

∫(1 -> 2) ∫(0 -> pi/2) θr drdθ
1/2 ∫(1 -> 2) θ(r^2)(0 -> pi/2) dθ
1/2 ∫(1 -> 2) θ(pi^2)/4 dθ
(pi^2)/8 ∫(1 -> 2) θ dθ
(pi^2)/16 (θ^2)(1 -> 2)
(pi^2)/16 (2^2 - 1^1)
(pi^2)/16 (4 - 1)
(pi^2)/16 (3)
3/16 pi^2

Any insight on what I did wrong?

 

[Stimpon]

Ah I think I didn't edit my post in time then, the upper limit should have been \frac{\pi}{4}, sorry. Your method is fine.

And just draw the lines y=0 and y=x and you should be able to see where y satisfies 0{\leq}y{\leq}x. Or think about it this way, where does (x,y) satisfy 0{\leq}y and where does it satisfy y{\leq}x. Then you just find the intersection of those two areas.

 

[DavidAp]

Ah I think I didn't edit my post in time then, the upper limit should have been \frac{\pi}{4}, sorry. Your method is fine.

And just draw the lines y=0 and y=x and you should be able to see where y satisfies 0{\leq}y{\leq}x. Or think about it this way, where does (x,y) satisfy 0{\leq}y and where does it satisfy y{\leq}x. Then you just find the intersection of those two areas.

Thank you so much, not just on this problem but on future problem to come! I never thought of visualizing it that way!