leslielau
- 8
- 0
Homework Statement
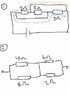
For 1 and 2 : Find the equivalent resistance for the resistor network provided
Homework Equations
For resistor in series : Req = R_{1}+R_{2}+...R_{n}
For resistors in parallel : Req = (1/R_{1}+1/R_{2}+... 1/R_{n})^{-1}
The Attempt at a Solution
For question 1 :
I have considered the two paths shown :
1st path (blue) : total resistance = 2 ohm
2nd path (orange) : total resistance = 2 ohm
so since these two paths are in parallel , Req = 1 ohm
But answer provided = 2/3 ohm
For Question 2 :
Since no current passes through the middle wire, upper path = 10 ohm
lower path = 10 ohm
So, total resistance = 5 ohm
However , the answer used the method of (1/4+1/8)^-1 + (1/2+1/6)^-1 = 4.17 ohm
But I don't understand this part, if there is current flowing in the middle wire, there would be one current flowing down and one current flowing up. Won't they cancel out each other? Thanks !