Electromagnetic induction and conducting rods

[apchemstudent]

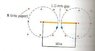
Two 0.68 m long conducting rods are rotating at the same speed in opposite directions, and both are perpendicular to a 4.7 T magnetic field. As the drawing shows, the ends of these rods come to within 1.0mm of each other as they rotate. More-over, the fixed ends about which the rods are rotating are connected by a wire, so these ends are at the same electric potential. If a potential difference of 4.5*10^3 V is required to cause a 1.0 mm spark in air, what is the angular speed (in rad/s) of the rods when a spark jumps across the gap?

Is it possible to still use the formula

Voltage potential = velocity * magnetic field * length of rod ?
v = r*angular speed

(4.5*10^3)/(4.7*.68) = v = r * angular speed

i got the angular speed as 2070 rad/sec. Is this correct how i solved the question? if not can you correct me. Thanks

 

[Astronuc]

Remember that the base of each rotating rod is at the same potential, but they move in opposite directions so that one will contribute V/2 and the other -V/2, and the potential difference is V = 4500 V.

 

[apchemstudent]

Remember that the base of each rotating rod is at the same potential, but they move in opposite directions so that one will contribute V/2 and the other -V/2, and the potential difference is V = 4500 V.

The answer in the back said 2100 rad/sec. At first i thought the same way with V/2, but i only got 1035 rad/sec. So doubling it will bring the answer closer. However though, is this the proper way to solve the problem, as posted from above?

 

[Andrew Mason]

Is it possible to still use the formula

Voltage potential = velocity * magnetic field * length of rod ? v = r*angular speed

Yes, but the speed is a function of l, so you have to apply a bit of calculus:

dE = vBdl \rightarrow E = \int_0^L \omega lBdl = \frac{1}{2}\omega BL^2

Note: the other rod is rotating with speed -\omega so the potential from the centre to the end is - \frac{1}{2}\omega BL^2

The condition for spark is Potential Difference = 4.5kV: E_L - E_R = 4,500.

AM

 

[Gamma]

Also note that one can avoid integration by dealing only with the angular velocity as it is independant of the length.

The angle swept by the rod in one second = \omega

So the area swept by the rod in one second, A=\frac{1}{2}L^2\omega

E = -\frac {d\phi} {dt} = -B\frac {dA} {dt}


E = -\frac {1} {2}BL^2\omega

Regards,
Gamma.