rhemmin
- 4
- 0
Homework Statement
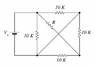
Find the current flowing through the voltage source in mA. Assume Vs = 3.9 V and R = 8.3 kohm. Round off your answer to two decimal points.
Homework Equations
1/R(equivalent) = 1/R1 + 1/R2 + ...
I=V/R
Kirchoff's voltage law
The Attempt at a Solution
I considered the 3 resistors in the upper left of diagram (10k, R=8.3k, 10k) to be in parallel and calculated their equivalent resistance to be 3.12 kOhms. I basically ignored the two 10kOhm resistors in the bottom right because a) they didn't seem to be in series, or parallel so I didn't know what to do with them and b) it seemed that the current would avoid them by taking the path of least resistance after going through the 3 resistors in parallel in the upper left. I then wrote the KVL equation: Vs - I(3.12*10^3) = 0 and solved for I determining the current to be 1.25mA.