- #1
Saladsamurai
- 3,020
- 7
So I got the diameter of the pin at a no problem. For some reason I am screwing up the Force at B. I thought my reasoning was correct, but I am coming up short. The answer is larger then what I an getting, so my F_BC must be too small, thus I am not accounting for something.
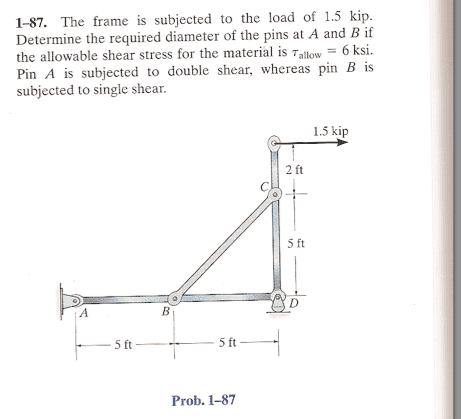
Here is my work:
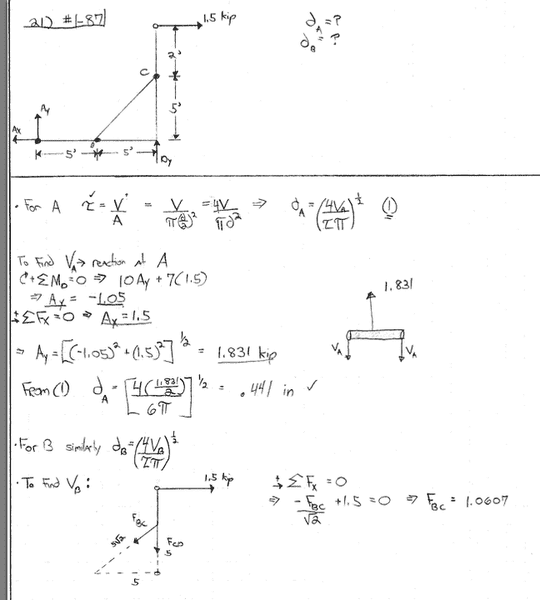
Here is my work:
