Mentz114 said:
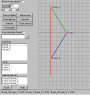
Rotating the diagram can bring any of the worldlines 'to rest', without changing the proper length of any segment of any worldline.
I disagree. Rotating the diagram will bring the world-line to a vertical, but the line of simultaneity associated with that worldline gets further away from the horizontal. The way you should bring a world-line "to rest" is a skew operation--not a rotation. You have to pull the line of simultaneity and the world-line in opposite directions.
On the other hand, you say by "rotating" you don't change the proper length. When you are rotating are you also rotating the axes of rotation along with the events? If so, then what you are doing is meaningless. You are turning the diagram to show it to someone else. If you rotate the event coordinates with respect to the x and t axes, you will certainly find that the proper time is not conserved.
Mentz114 said:
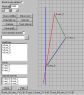
There is no 'now' on the diagram, unless you choose one by drawing a horizontal line, which defines a common parameter time (t) value.
There is a difference in the way we think of it that comes clear when I compare your space-time demonstration application to my space-time application.
In your space-time diagram, you have a button that runs the simulation, whereupon you let t go from -10 to +10 and watch the events unfold, as they happen.
In my space-time diagram, on the other hand, upon clicking the "pass-time" button, the computer begins decrementing the time coordinate of every event, so they go from the future, into the present, and then into the past. I have a distinct origin at (0,0) which represents "here and now."
Now both of us use the same origin for the Lorentz Transformation, but in yours, you have an origin that never moves. By decrementing the time coordinate of all of the events over time, I am constantly changing the "now."
It's a difference in convention: for yours, "now" progresses from the negative to the positive. For mine "now" stays at t=0, while the events progress from the future, to the present, to the past.
Jonathan