How to Minimize Oscillation Amplitude in a Damped Driven Oscillator?

[barakudaxxl]

Homework Statement

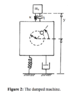
I have a project in university that's about creating a simplified model of a washing machine in the program ADAMs View. Here is a picture of how it's constructed: https://imgur.com/a/zZzS5

So basically to oversimplify the problem I've understood that the rotating mass will cause a force on the machine resulting in a damped driven harmonic oscillation. If we take a look at the bottom of the machine there is damper and a spring. The damper constant and the spring constant are both fixed values given to us. (spring constant k = 9,35*10⁶ N/m and damping constant c = 3000 Ns/m): We are also given the mass of the machine m_h, mass of rotor m_r and the velocity of rotor ω.

The problem to solve is to design the upper part (the second spring and damper) of the machine to minimize the amplitude of the machine's oscillation. We have three parameters that we have to vary. K being the spring constant, n being the damping constant and being the mass (where m_a≤10 kg)

Using ADAMS and running simulations when I vary one factor at a time I have come to the conclusion that m_a being as high as possible (10 kg), n being as low as possible (=0) and K being around 10⁶ N/m will result in a small amplitude.

Homework Equations

I have derived the equation of motion for the washing machine and the damper and spring on the bottom from the free body diagram of the machine, not taking into consideration the upper damper and spring because this was the first part of the project.

x''+2ξω_{n}x' + ω_{n}x = \frac{F_{0}}{m}sin(ωt+φ_{0}) + \frac{kx_{0}}{m} where 2ξω_{n}=\frac{c}{m}, ω_{n}^2=\frac{k}{m}, F_{0}=m_{r}eω^2, m=m_{h}+m_{r}

(I'm from Sweden so if these formulas dosen't look exactly the same in your country then I think that's the reason.)

The Attempt at a Solution

Aside from the conclusions above I have to derive a strategy for this optimal design (minimize the amplitude), explaining what's happening using formulas. To minimize this amplitude I think I need to explain what's happening with the superposition principle. There must be destructive interference but my problem is between what parts of this system. The upper part really complicates things for me and this is the part where I would like some help.

I'm very grateful for every tip! Thanks.

 

[BvU]

Hello bog one,

please sort out and list your variables a bit more clearly: I get confused if you first write a given c and then write

n being the damping constant

n being as low as possible (=0)

Also seeing y as coordinate in the picture and x in the equations does not help, even if x=y in Sweden

[edit] copied in the picture -- imgur isn't all that sustainable

 

[barakudaxxl]

Hello bog one,

please sort out and list your variables a bit more clearly: I get confused if you first write a given c and then write
Also seeing y as coordinate in the picture and x in the equations does not help, even if x=y in Sweden

View attachment 221740

[edit] copied in the picture -- imgur isn't all that sustainable

The project is is separated into two parts. The first part is this photo: https://imgur.com/rHrWjxL. It's actually in the other link also. It's consisting of the washing machine and the damper and spring at the bottom. C is the damping constant for that damper and not the one above. n is the damping constant of the damper located at the top of the machine,
My equation of motion is for only this system and in the picture you can see that x is the coordinate.

The second part is this picture you are referring to https://imgur.com/hCMLepR. My problem is with this part.

 

[BvU]

My bad for missing the second picture , the one from the first part of the exercise.
Helps a lot.

I see an $\eta$ instead of an n and a $\kappa$ instead of a K in the first picture (the one from the second part of the exercise).

Now I can follow the equation for $x$, except I don't see why it has an $\omega_n$ instead of an $\omega$ and I think a square dropped out of the third term.

First part of the exercise yields you an amplitude $A$ for the steady state solution (right?) and I gather the exercise wants you to size $m_a$, $\kappa$ and $\eta$ in such a way that that $A$ is reduced to a minimum (right?).

And you use the ADAMs program as a kind of integrator for the coupled oscillators (to find a minimum by trial and error ?), or do you set up the full set of equations of motion for both $x$ and $y$ (including the coupling terms) ?

 

[barakudaxxl]

I see an η instead of an n and a κ instead of a K in the first picture (the one from the second part of the exercise).

That't correct it's my fault. I didn't know how to write these letters so I wrote n and K instead.

Now I can follow the equation for x, except I don't see why it has an ω_n instead of an ω and I think a square dropped out of the third term.

We use ω_nin the third term. I've seen on e.g. Wikipedia that it's ω_0 instead but it's the same. In the third term I did forgot a square it should be ω^2_n.

First part of the exercise yields you an amplitude A for the steady state solution (right?) and I gather the exercise wants you to size m_a, κ and η in such a way that that A is reduced to a minimum (right?).

. That's right. I have to find values of m_a, κ and η in such a way that that A is reduced to a minimum.

nd you use the ADAMs program as a kind of integrator for the coupled oscillators (to find a minimum by trial and error ?), or do you set up the full set of equations of motion for both x and y (including the coupling terms) ?

I use ADAMs to find a correlation between m_a, κ and η so A is reduced to a minimum. I do this by simulating my built model and varying each value one by one but I also have to find a correlation between these values using maybe a formula of some sort. I don't think it's necessary to find out the equation of motion for y too. My instinct says that minimizing of the amplitude A has to do with destructive interference between the rotor and the spring-damper system on top of the machine