cooltwins
- 3
- 0
Homework Statement
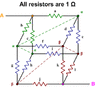
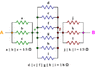
each edge of a cube is built with a one ohm resistor, body diagonals are also built with one ohm resistors each. find out equivalent resistance across any two adjacent vertices.
Homework Equations
i guess it deals with star and delta transformations
The Attempt at a Solution
i'm attempting the question at the present and will post my solution once I'm done with the question.
hoping for a reply from you,
cheers
cooltwins