archaic
- 688
- 214
- Homework Statement
- A 0.140-kg, 45.4-cm-long uniform bar has a small 0.050-kg mass glued to its left end and a small 0.100-kg mass glued to the other end. You want to balance this system horizontally on a fulcrum placed just under its center of gravity.
How far from the left end should the fulcrum be placed?
- Relevant Equations
- ##\sum\tau=0##
I don't understand the question; they're telling me that the fulcrum is just under the center of gravity of the bar, but that I also need to find its position.
In any case, I suppose that the fulcrum's position is ##x##.
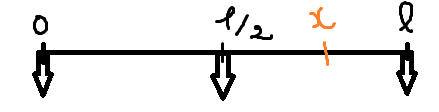
Let the weight at the left end be ##w_1##, at the right end be ##w_2##, and of the center of gravity be ##w##.
Since ##w_2>w_1##, I'm going to suppose that ##x>\frac l2##.
$$w(x-\frac l2)+w_1x=w_2(l-x)\\x=l\frac{w_2+\frac w2}{w+w_1+w_2}=45.4\times\frac{0.100+\frac{0.140}{2}}{0.140+0.100+0.050}$$
In any case, I suppose that the fulcrum's position is ##x##.
Let the weight at the left end be ##w_1##, at the right end be ##w_2##, and of the center of gravity be ##w##.
Since ##w_2>w_1##, I'm going to suppose that ##x>\frac l2##.
$$w(x-\frac l2)+w_1x=w_2(l-x)\\x=l\frac{w_2+\frac w2}{w+w_1+w_2}=45.4\times\frac{0.100+\frac{0.140}{2}}{0.140+0.100+0.050}$$