jra_1574
- 12
- 0
Hello Everyone!
i need some guide and hints about this...
Here is the link for the picture...
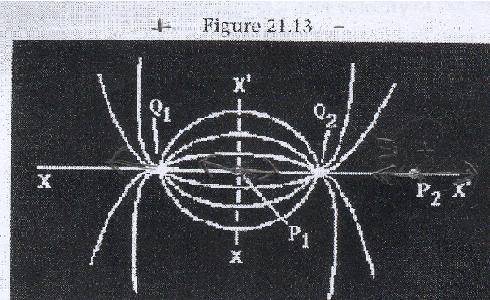
From the figure, the electric Field lines arising from two charges Q1 and Q2 are shown. From this drawing we can see that
A) The electric field could be zero at P2
B) Both Q1 and Q2 have the same sign
C) |Q1|>|Q2|
D) the electric field could be zero at P1
E) none of these is true
Something is telling me that B is not true... why?
the lines go from one to the other, if they were from the same sign the lines would go apart from one another...now C... we can't tell because we don't know which one is proton and which is the electron. Choice E i don't think so..
So it must be either A or D, but i don't know which one and why...
can anyone help me here please?
Thanks!
i need some guide and hints about this...
Here is the link for the picture...
From the figure, the electric Field lines arising from two charges Q1 and Q2 are shown. From this drawing we can see that
A) The electric field could be zero at P2
B) Both Q1 and Q2 have the same sign
C) |Q1|>|Q2|
D) the electric field could be zero at P1
E) none of these is true
Something is telling me that B is not true... why?
the lines go from one to the other, if they were from the same sign the lines would go apart from one another...now C... we can't tell because we don't know which one is proton and which is the electron. Choice E i don't think so..
So it must be either A or D, but i don't know which one and why...
can anyone help me here please?
Thanks!