Baxidur
- 8
- 0
Hi
First off I'm not a student, this is purely a curiosity question
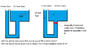
In pascals law classic drawing if you added a piston inside one of the cylinders what would happen?
I've added a drawing to clarify
I'm totally split on what the answer is, Pascals law seems to state the pressure on both sides of the piston will be equal, but real life seems to say the weight of the water in B will push the piston down
Thanks in advance for any help
First off I'm not a student, this is purely a curiosity question
In pascals law classic drawing if you added a piston inside one of the cylinders what would happen?
I've added a drawing to clarify
I'm totally split on what the answer is, Pascals law seems to state the pressure on both sides of the piston will be equal, but real life seems to say the weight of the water in B will push the piston down
Thanks in advance for any help