PTPM93
- 4
- 0
Homework Statement
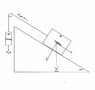
A large block is being dragged up a ramp by a block falling due to gravity over a pulley. The large block has a mass of 1400kg and the smaller block suspended has a mass of 530kg. The coefficient of kinetic friction between the large block and the ramp is 0.13. The ramp is at an angle of 15degrees
what is the acceleration of the block up the ramp?
Homework Equations
F=ma
Ff=ukN
The Attempt at a Solution
I know there are four forces actnig on the block, and these are:
in the negative x direction there is the mass of the big block * gravity *sin15 + Ff (m*g*sin15 + 0.13*m*g*cos15)
and in the positive x direction there is the smaller block pulling it down via gravity so m*g*sin15 (m in this case is the smaller block)
a=fnet/m where fnet= mlittle*g*sin15 -(mbig*g*sin15 + 0.13*mbig*g*cos15)
The problem is it ends up being negative when I go to do, and I'm sure the block is mean to be accelerating up the ramp.
a=Fnet/m