Potential well Definition and 218 Threads
-
J
Undergrad A definition of a Potential Well
Hello I read the following sentence when reading about ion traps: "By changing the trapping voltage we are changing the depth of the potential trapping well, therefore at the same axial position there is a corresponding increase in the potential well, which means that the ion will have to... -
M
How do we observe an elextron in a potential well ?
Homework Statement It's problem on the uncertainty principle. It is as follows: Suppose we have confined an electron in an infinite potential well of length L=1A . Say that this electron is in the ground state of the well. Now, say that we wish to observe the electron with accuracy of 0.2A...- MariosB
- Thread
- Potential Potential well
- Replies: 1
- Forum: Advanced Physics Homework Help
-
R
Probability of finding particle in 1D finite potential well
Homework Statement ψx is the function of postion for a particle inside a 1D finite square well. Write down the expression for finding the particle a≤x≤b. Do not assume that ψx is normalised. Homework Equations The Attempt at a Solution This is to check I'm not going insane: P...- Ryomega
- Thread
- 1d Finite Particle Potential Potential well Probability
- Replies: 20
- Forum: Introductory Physics Homework Help
-
R
Ground State Energy for infinte potential well
Homework Statement A particle of mass (m) moves in the one-dimensional potential V(x) = V0 0 ≤ x ≤ a = ∞ otherwise Wave function of the particle is ψ(x,t) = C sin (\frac{x\pi}{a}exp[-iωt] Determine V0 Homework Equations Schrödinger's Equations...- Ryomega
- Thread
- Energy Ground Ground state Ground state energy Potential Potential well State
- Replies: 5
- Forum: Introductory Physics Homework Help
-
T
Triangular Potential Well
Homework Statement find Transmission and Reflection coefficients (QM) for the following triangular potential well: U=U_{0}(1-\frac{x}{a}) : x\geq0 and U= 0 : x<0 and U_{0}>0 , a>0 Homework Equations The Attempt at a Solution Basically constructing the wave functions is...- TMSxPhyFor
- Thread
- Potential Potential well
- Replies: 1
- Forum: Advanced Physics Homework Help
-
P
Infinite potential well energy question
Homework Statement A particle of mass m is confined (in one dimension) to the region 0 ≤ x ≤ a by a potential which is zero inside the region and infinitely large outside. If the wavefunction at time t = 0 is of the form ψ (x,0) = Ax(a - x) inside the region ψ (x, 0) = 0 outside the...- phys2
- Thread
- Energy Infinite Infinite potential well Potential Potential well
- Replies: 2
- Forum: Advanced Physics Homework Help
-
P
Undergrad Energy values in infinite potential well
I was wondering why the spacing between energy values keep increasing for the infinite potential well?- phys2
- Thread
- Energy Infinite Infinite potential well Potential Potential well
- Replies: 2
- Forum: Quantum Physics
-
P
Potential well with inner step, perturbation theory
hey, say you have a infinite potential well of length L, in the middle of the well a potential step of potential V and length x. Inside the well is a particle of mass m. why are the first order energy corrections large for even eigenstates compared to odd ones? also, say well...- physicsjock
- Thread
- Perturbation Perturbation theory Potential Potential well Theory
- Replies: 6
- Forum: Advanced Physics Homework Help
-
F
Position of particle in infinite potential well
Homework Statement For the case n=1, calculate the probability that the particle is found in within the region a/4<x<3a/4 (n is the energy level, a is the width of the infinite potential well). Compare this result with the case n=8 and with the classical result. Homework Equations...- Froskoy
- Thread
- Infinite Infinite potential well Particle Position Potential Potential well
- Replies: 2
- Forum: Introductory Physics Homework Help
-
P
Finite Well Solutions: Understanding d and k in Potential Wells
Hey, I've been trying to work out how, for a finite well of high Vo and width L, the interior solution has the form L Sin(kx + d), I see that if d=0 then the solution resembles an infinite well, so that implies d depends inversely on the wells potential. But I can't work out what d comes...- physicsjock
- Thread
- Potential Potential well
- Replies: 4
- Forum: Advanced Physics Homework Help
-
P
Potential well solutions question
http://img138.imageshack.us/img138/7762/asdhl.jpg Thanks in advance- physicsjock
- Thread
- Potential Potential well
- Replies: 1
- Forum: Introductory Physics Homework Help
-
A
Finding the potential of a 1d finite square potential well
Homework Statement The deuterium nucleus (a bound state of a proton and a neutron) has one bound state. The force acting between a proton and a neutron has a strong repulsive component of range 0.4 fm and an attractive component of range ~2.4 fm. The energy needed to separate the neutron from...- AlKhalicious
- Thread
- 1d Finite Potential Potential well Square
- Replies: 1
- Forum: Advanced Physics Homework Help
-
S
Probability current inside the barrier of a finitie square potential well
if ψ=C*e^(kx) + D*e^(-kx) show that the probability current density is Jx=(i*k*hbar/m)[c*conj(D) - conj(C)*D] since Jx= (i*hbar/2m)*[ψ * derivative of conj(ψ) - conj(ψ)*derivative of ψ] ψ=C*e^(kx) + D*e^(-kx) conj(ψ)= conj(C)*e^(-kx) + conj(D)*e^(kx) ψ ' = C*k*e^(kx) - D*K*e^(-kx)...- StephenD420
- Thread
- Current Potential Potential well Probability Square
- Replies: 1
- Forum: Introductory Physics Homework Help
-
M
Particle in a triangular potential well
Homework Statement Particle is in a potential well in the shape of a isosceles right-angled triangle. Need to find the wave function and allowed energies. Homework Equations How to determinate a boundaries for the potential when that line is in a form of some linear function, there is no...- masterjoda
- Thread
- Particle Potential Potential well
- Replies: 16
- Forum: Advanced Physics Homework Help
-
S
Electron in a potential well of specified thickness
an electron in a potential well of thickness (e.g 1nm) with infinitly high potential barriers. it is in the lowest possible energy state. to calculate the energy of the electron. i used: E=(n^2 pi^2 h(bar)^2)/ (2m Lz^2) which will result in approx 10E-19 j my question is, how can...- solas99
- Thread
- Electron Potential Potential well Thickness
- Replies: 1
- Forum: Advanced Physics Homework Help
-
I
Graduate What Are Potential Wells in Lennard Jones Potential?
Hi PF users, The subject of this thread is clearly stated on the title ( above). So my question is what is mean't by a 'potential well'. I have a question based on Lennard jones potential from where this question arose in the first place ( which I will probably post on respective...- ibysaiyan
- Thread
- Potential Potential well
- Replies: 4
- Forum: Quantum Physics
-

Graduate Calculating the Potential Well of Neutron Capture by the Strong Force
If I have a low energy neutron and I bring it close to a nucleus it will be captured when it gets close enough. How can I calculate the shape of the potential well of the nucleus for neutron capture? I keep reading that it is due to the strong force, which I agree with. But it is some...- edpell
- Thread
- Capture Force Neutron Neutron capture Potential Potential well Strong force
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-

Rectangular finite potential well problem
Homework Statement An electron enters in a finite rectangular potential well of length 4 angstroms. When the entering electrons have a kinetic energy of 0.7 eV they can travel through the region without having any reflection. Use this information to calculate the depth of the potential well...- fluidistic
- Thread
- Finite Potential Potential well Rectangular
- Replies: 2
- Forum: Advanced Physics Homework Help
-
L
Wave Functions in a Potential Well with infinite high walls
Homework Statement Consider a potential well with infinite high walls, i.e. V(x)=0 for -L/2\leq x \leq +L/2 and V(x)=\infty at any other x. Consider this problem (the first task was to solve the stationary Schroedinger equation, to get the Energies and Wave Functions, especially for n=1 and...- Lunar_Lander
- Thread
- Functions Infinite Potential Potential well Wave Wave functions
- Replies: 1
- Forum: Advanced Physics Homework Help
-
M
Challenging Semi-Infinite Potential Well Problem
Homework Statement "Use the semi - infinite well potential to model a deuteron, a nucleus consisting of a neutron and a proton. Let the well width L be 3.5 x 10^-15 meters and V - E = 2.2 MeV. Determine the energy E, and determine how many excited states there are."Homework Equations Since V >>...- mancini0
- Thread
- Potential Potential well
- Replies: 5
- Forum: Advanced Physics Homework Help
-
Undergrad Why did the sphere in a potential well stop rolling sooner than expected?
Imagine you put a sphere on a track which is part of a vertical circle.You expect the sphere to roll in a path like a pendulum.it should do it like a mass on an almost frictionless surface because the friction of the surface is rolling the sphere not stopping it and the air drag isn't very high... -
L
Particle in semi infinite potential well
Homework Statement particle moving in the semi infinite potentail well set up and solve SE for the system assume E<VoHomework Equations (-h2/2m) d2\psi/dx2 +v(x)\psi=E\psiThe Attempt at a Solution so in reagion one its infinite so \psi=0. reagion 2 is what i am confused about. looking through...- leonne
- Thread
- Infinite Infinite potential well Particle Potential Potential well
- Replies: 2
- Forum: Advanced Physics Homework Help
-
H
Identical particles in a 2D potential well
Homework Statement So, I'm asking for a bit of help before I confuse myself completely. The question statement is: Consider a two-dimensional potentialbox V(x,y) = 0 if 0 \leq x \leq a, 0 \leq y \leq 2a and infinity otherwise. a) Determine the energy eigenstates and energy...- Hannisch
- Thread
- 2d Identical particles Particles Potential Potential well
- Replies: 5
- Forum: Advanced Physics Homework Help
-
H
Analysis of Finite Square Potential Well: Bound and Scattering States
Hello, can anyone explain the full analysis of finite square potential well (bound state and scattering state) if V(x) = -Vo, x <= 0 (region 1) V(x) = 0, 0 < x < a (region 2) V(x) = -Vo, x >= a (region 3) It will be helpful if you can attach the analysis in .pdf format. Thank you in...- Hydeyuki
- Thread
- Finite Potential Potential well Square
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Quantum mechanics, potential well
Homework Statement A particle of mass m is find to be inside a uni-dimensional potential well of the form: V(x)=0 for x \leq -a and a\leq x and V(x)=-V_0 for -a <x<a. 1)Write down the corresponding Schrödinger's equation. 2)Consider the case -V_0<E<0. Determine the contour conditions and...- fluidistic
- Thread
- Mechanics Potential Potential well Quantum Quantum mechanics
- Replies: 41
- Forum: Advanced Physics Homework Help
-
N
Graduate 1D delta funtion potential well
Hello forum, I have a question regarding the delta function potential well. Given the following potential: V(x) = -αδ(x) for -a/2 < x < a/2 (α- positive constant) and V(x) = 0 elsewhere, how would one show that the ground state is the only eigenstate with E <0. One could of course solve the...- Nemetz
- Thread
- 1d Delta Potential Potential well
- Replies: 8
- Forum: Quantum Physics
-
T
Wavelength in finite potential well
Homework Statement 1)The graph below represents the ground state wave function of an electron in a finite square well potential of width L. The potential is zero at x = 0. The wave function of the electron within the well is of the form A cos( 2πx / λ ) where A is a normalization...- Thefox14
- Thread
- Finite Potential Potential well Wavelength
- Replies: 4
- Forum: Advanced Physics Homework Help
-
N
Infinite potential well- Delta potential inside
Hello again. Thank you guys. You have been great help... I have another one: Given a potential well- 2a is it's width, and in the middle - there is a delta potential: V(x)= \frac {\hbar^2} {2m} \frac {\lambda} {a} \delta(x) I am looking for the odd solution to this problem. I thought...- noamriemer
- Thread
- Delta Infinite Infinite potential well Potential Potential well
- Replies: 1
- Forum: Advanced Physics Homework Help
-
F
Finite potential well easy question
Homework Statement 1.) A particle of kinetic energy 50 eV in free space travels into a region with a potential well of depth 40 eV. What happens to its speed? a.) it stays the same b) it increases in the region of the well c) it decreases in the region of the well d) not enough information...- frozenguy
- Thread
- Finite Potential Potential well
- Replies: 2
- Forum: Introductory Physics Homework Help
-
R
Boundary conditions in finite potential well
Homework Statement Hi guys, I'm having trouble understanding the finite potential well, in particular the boundary conditions The well under scrutiny has potential V(x)= 0 for |x|<a and V(x)=V_0 for >a Homework Equations \frac{d^2\psi}{dx^2}=-\sqrt{\frac{2mE}{\hbar^2}}\psi=-\alpha^2\psi...- Ritorufon
- Thread
- Boundary Boundary conditions Conditions Finite Potential Potential well
- Replies: 2
- Forum: Advanced Physics Homework Help
-
C
Potential well, limits changed, quantum
Homework Statement If you have a 1d infinite potential well between 0 and a which is then expanded to become 0 -2a with the wavefunction in that instant undisturbed, what is the expectation value of energy at that moment. my thoughts are that as the eigenfunction will be the same then...- Chronos000
- Thread
- Limits Potential Potential well Quantum
- Replies: 7
- Forum: Advanced Physics Homework Help
-
D
Double Delta Function Potential Well
Hello Again! My question: Find the bound energy spectrum of the potential that contains two delta-function wells: V(x) = -V_{0}\delta(x-\frac{a}{2}) -V_{0}\delta(x+\frac{a}{2}) under the assumption that the wells are located very far away from each other. Find and plot the associated stationary...- doublemint
- Thread
- Delta Delta function Delta function potential Function Potential Potential well
- Replies: 16
- Forum: Advanced Physics Homework Help
-
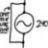
Free Electron passing over Potential Well
Homework Statement See figure attached. Homework Equations The Attempt at a Solution What condition must be satisfied in order for the electron to pass over the well? Thanks again!- jegues
- Thread
- Electron Potential Potential well
- Replies: 6
- Forum: Introductory Physics Homework Help
-
A
Energy levels for two particles in infinite potential well
problem is: (a)write down the spatial or orbital for two-non interacting particles, with the same mass, in a one dimensional well, where the potential energy is zero for 0<x<2a and infinite anywhere else. (b)What are the energies of the four lowest energy levels for the system in units of...- AStaunton
- Thread
- Energy Energy levels Infinite Infinite potential well Levels Particles Potential Potential well
- Replies: 6
- Forum: Advanced Physics Homework Help
-
L
How Does an Electron Impact the Walls of an Infinite Potential Well?
Homework Statement An electron is confined to an infinite potential well of width L. Find the force it exerts on the walls of the well in the lowest energy state: a) Estimate the force using uncertainty principle b) Calculate the force exactly for the ground-state wavefunction Homework...- laxatives
- Thread
- Infinite Infinite potential well Potential Potential well
- Replies: 1
- Forum: Introductory Physics Homework Help
-
D
Heaviside step fn in infinite potential well
By considering the wavefunctions within the potential described below, determine the incident, reflected and transmitted amplitudes of each part of the wavefunction at the step boundary (as necessary). For x<0, V = infinity. For 0<x<a, V = 0 For a<x<L, V = V1 For x>L, V = infinity...- davo789
- Thread
- Heaviside Infinite Infinite potential well Potential Potential well
- Replies: 15
- Forum: Advanced Physics Homework Help
-
B
Fermi Energy of Non-Interacting Identical Li Atoms in a 3D Harmonic Potential Well
Homework Statement The degeneracy of the nth level above the ground state for a three dimensional harmonic oscillator is (n+1)(n+2)/2 where n takes values n=0,1,2,... A gas of N non-interacting identical lithium atoms (mass 6amu) each having spin1/2 is confined in a 3d harmonic potential...- bon
- Thread
- 3d Atoms Energy Fermi Fermi energy Harmonic Potential Potential well
- Replies: 7
- Forum: Advanced Physics Homework Help
-
S
Finite potential well- well's depth?
Homework Statement The problem is to find a well's depth Vo that the electron which is trapped inside has two stable states. Well starts at x=0 and ends at x=L. Homework Equations The Attempt at a Solution I tried to solve Schrödinger equation for each area (x<0 0<x<L x>L) but...- Someone88
- Thread
- Depth Finite Potential Potential well
- Replies: 12
- Forum: Advanced Physics Homework Help
-
C
Calculating % Contribution of nth Wavefunction in Potential Well
Homework Statement What fraction (as a percentage) does the n=(2x2-1)th infinite potential well wavefunction contribute to the 'classical' initial wavefunction psi(x,t=0)=1/sqrt(L) ? (Why are the even n excluded?) Homework Equations psi(x,t=0) = 1 / sqrt(L) The Attempt at a Solution...- Caldo120
- Thread
- Potential Potential well Wavefunction
- Replies: 1
- Forum: Advanced Physics Homework Help
-
N
Graduate Non spherical solutions of a spherical potential well?
Hi all just a question about the understanding of the solutions of a spherical potential well. What is the physical sense of solutions which have no spherical symmetry? I just would think that the probability of finding a particle whose state is described by one of the eigenstate of the...- nista
- Thread
- Potential Potential well Spherical
- Replies: 1
- Forum: Quantum Physics
-
G
Graduate Electrons traversing a Potential well
Let's imagine an electron that lives in an one dimensional world where there is a potential well near x=0 and that for x=+inf or -inf the electron is free. Is there any relation between the transmission coefficient of an electron arriving at the well coming from x=-inf and the transmission...- go quantum!
- Thread
- Electrons Potential Potential well
- Replies: 2
- Forum: Quantum Physics
-
A
Quantum Infinite Potential Well - Probability of Ground-State Energy
Homework Statement A particle in the infinite potential well in the region 0 < x < L is in the state \psi(x) = \begin{cases} Nx(x-L) & \text{ if } 0<x<L \\ 0 & \text{ if } otherwise \end{cases} a) Determine the value of N so that the state is properly normalised b) What is the...- ARasmussen
- Thread
- Energy Infinite Infinite potential well Potential Potential well Probability Quantum
- Replies: 3
- Forum: Advanced Physics Homework Help
-
F
Schrodinger Equation for Potential Well
Homework Statement A particle of mass m and total energy E < 0 is confined to a potential given by: where \alpha is some positive constant. Show that the wavefunction is a solution of the time independent Schrödinger equation when x > 0. Find the associated energy Eigenvalue E.Homework...- freddy_12345
- Thread
- Potential Potential well Schrödinger Schrodinger equation
- Replies: 1
- Forum: Advanced Physics Homework Help
-
E
Probability for finding particle outside potential well
Homework Statement A particle in the harmonic oscillator potential is in the first excited state. What is the probability of finding this particle in the classically forbidden region? Homework Equations probability of finding particle = integral of abs[psi squared] [a,b] The Attempt...- Eric_meyers
- Thread
- Outside Particle Potential Potential well Probability
- Replies: 3
- Forum: Advanced Physics Homework Help
-
I
Classical vs quantum infinite potential well
Homework Statement This is a problem from Merzbacher. Assuming a particle to be in one of the stationary states of an infinitely high one-dimensional box, calculate the uncertainties in position and momentum, and show that they agree with the Heisenberg uncertainty relation. Also show that...- IHateMayonnaise
- Thread
- Classical Infinite Infinite potential well Potential Potential well Quantum
- Replies: 2
- Forum: Advanced Physics Homework Help
-

Graduate Bizarre results of 1-dimensional delta-function potential well
I was curious what a delta-function potential barrier would do to a free (E>0) 1-dimensional particle, so I figured it out. I used V = b δ(x) for the potential energy. I got the expected result that full reflection will occur as |b|→∞ or as E→0. These results make sense intuitively when b>0. My...- bknock
- Thread
- Potential Potential well
- Replies: 8
- Forum: Quantum Physics
-
R
Graduate What is excursion of a potential well?
What is "excursion" of a potential well? I think it means maximum depth of the well, but I've never heard this term before and I might be wrong. I don't have much of a quantum mechanics background. Details: I'm reading and implementing "Solution of the Schrödinger Equation by a Spectral...- rcompton
- Thread
- Potential Potential well
- Replies: 3
- Forum: Quantum Physics
-
P
Graduate Looking for an analytical solution for a quadratic attractive potential well
I am trying to derive an equation of motion for a simple electrostatic potential well. Imagine a scenario where an electron (or other charged particle) is released from an arbitrary distance from a fixed (unperturbable) attractive charge (say a proton fixed in space). In 1 dimension, the... -
M
Solve Double Potential Well: Write Equations & Find Wavenumbers
Homework Statement V(x) = \left\{\infty \textrm{ for } x<0 \left\{0 \textrm{ for } 0<x<a \left\{V_0 \textrm{ for } a<x<a+2b \left\{0 \textrm{ for } a+2bx<2a+2b \left\{\infty \textrm{ for } 2a+2b<x Set up the relevant equations in each region, write down the appropriate solution and...- MobiusPrime
- Thread
- Potential Potential well
- Replies: 4
- Forum: Advanced Physics Homework Help
-
A
Finite/Infinite Potential Well Problems
Hi, (first ever post) I have the following three problems 1) A particle is in the ground state of an infinite well from 0<x<a. Find the probability that it is in the middle half of the well. I think I have managed this, its just the integral of the wave function squared then I put in the...- Anonymous1783
- Thread
- Potential Potential well
- Replies: 4
- Forum: Introductory Physics Homework Help