What is Symmetric: Definition and 563 Discussions

Symmetry (from Greek συμμετρία symmetria "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article.
Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music.This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and nature; and in the arts, covering architecture, art and music.
The opposite of symmetry is asymmetry, which refers to the absence or a violation of symmetry.

View More On Wikipedia.org
Recent contents Top users
  1. looseleaf

    I Triplet State Symmetric Wavefunction

    Hi everybody. I was reading about the singlet and triplet states. It makes sense that we use an antisymmetric wavefunction for the singlet state, as we are talking about two fermions. But why are we using a symmetric wavefunction for the Sz = 0 triplet state? Doesn't this go against the...
  2. D

    I Square of determinant is symmetric

    This property is given in my book. The square of any determinant is a symmetric determinant. Well it works when I take a determinant say 3x3 and multiply it by itself using row to row multiplication. But it fails if I multiply using row to column. Thanks
  3. odietrich

    I General form of symmetric 3x3 matrix with only 2 eigenvalues

    I'm looking for the general form of a symmetric 3×3 matrix (or tensor) ##\textbf{A}## with only two different eigenvalues, i.e. of a matrix with the diagonalized form ##\textbf{D}=\begin{pmatrix}a& 0 & 0\\0 & b & 0\\0 & 0 & b\end{pmatrix} = \text{diag}(a,b,b)##. In general, such a matrix can be...
  4. H

    Cubic polynomial for the motion of a heavy symmetric top

    In the second paragraph after the expression of ##f(u)## below, it wrote "there are three roots to a cubic equation and three combinations of solutions". However, the combination of having three equal real roots was not mentioned. Why? In the next paragraph, in the second sentence, it wrote "at...
  5. N

    I Is the influence of dark matter symmetric?

    I am more familiar with quantum physics than cosmology so it occurred to me that I hadn't heard anyone talk about the question of symmetry with respect to dark matter. If its influence is restricted to the disc of a galaxy, but it is particle-like in structure than symmetry is violated isn't...
  6. P

    QR factorization for a 4x4 tridiagonal symmetric matrix

    Homework Statement $$\begin{bmatrix} a_{11} & a_{12} & 0 & 0\\ a_{12} & a_{22} & a_{23} & 0\\ 0 & a_{23} & a_{33} & a_{34} \\ 0 & 0 & a_{34} & a_{44} \\ \end{bmatrix} = \begin{bmatrix} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ q_{31} & q_{32} & q_{33} & q_{34}...
  7. physkim

    Engineering Symmetric Operation in Circuits

    Homework Statement For the characteristic curves shown below, select resistors for an H-biased common emitter amplifier for symmetric operation. Show the load line and operating pointing on the graph Homework Equations What does it mean by "symmetric operation"? The Attempt at a Solution...
  8. throneoo

    Spherically symmetric Heat Equation

    Homework Statement A ball of radius a, originally at T0, is immersed to boiling water at T1 at t=0. From t≥0, the surface (of the ball) is kept at T1 Define u(r,t)=R(r)Q(t)=T(r,t)-T1 ΔT=T0-T1<0 r,t≥0 Homework Equations ∇2u=r-2 ∂/∂r ( r2 ∂u/∂r ) =D-1∂u/∂t D>0 The Attempt at a Solution...
  9. RJLiberator

    Abstract Algebra: Bijection, Isomorphism, Symmetric Sets

    Homework Statement Suppose X is a set with n elements. Prove that Bij(X) ≅ S_n. Homework Equations S_n = Symmetric set ≅ = isomorphism Definition: Let G and G2 be groups. G and G2 are called Isomorphic if there exists a bijection ϑ:G->G2 such that for all x,y∈G, ϑ(xy) = ϑ(x)ϑ(y) where the...
  10. M

    1d diffusion equation solution for slab with non symmetric source

    Disclaimer: This is a homework problem I need to analytically solve the diffusion equation for a 1d 1 group slab with width a, and source distribution Se^(-k(x+a/2)) I've gone through the math, and come up with my homogeneous and particular solution and attempted to apply the boundary...
  11. Estanho

    I Symmetric injective mapping from N² to N

    Hi, I've been trying to find one symmetric "injective" N²->N function, but could not find any. The quotes are there because the function I'm trying to find is not really injective, as I need that the two arguments be interchangeable and the value remains the same. In other words, the tuple (a...
  12. M

    MHB Symmetric Polynomials s1,s2,s3

    Express r12+r22+...+rn2 as a polynomial in the elementary symmetric polynomials s1, s2, . . . ,sn. I'm sure the equation we are dealing with is (r1+r2+...+rn)2 which is very large to factor out but should yield r12+r22+...+rn2+(other terms) I believe s1=r1+r2+...+rn s2=Σri1ri2 for...
  13. M

    MHB Symmetric Polynomials Involving Discriminant Poly

    Question: Let τ = (i, j) ∈ Sn with 1 ≤ i < j ≤ n. Prove: δ(rτ(1) , . . . ,rτ(n) ) = −δ(r1, . . . ,rn) Note: Discriminant Polynomial δ(r1,r2,...,rn) = ∏ (ri - rj) for i<j I am pretty confused on where to begin. Based on the note, does −δ(r1, . . . ,rn) then =...
  14. G

    MHB S3 Group Symmetry: $(xy)^2 \ne x^2y^2$ Example

    Problem: In $S_3$ give an example of two elements $x$ and $y$ such that $(xy)^2 \ne x^2y^2$. Attempt: Consider the mapping $\phi: x_1 \mapsto x_2, x_2 \mapsto x_1, x_3 \mapsto x_3$ and the mapping $\psi: x_1 \mapsto x_2, x_2 \mapsto x_3, x_3 \mapsto x_1$. We have that the elements $\phi, \psi...
  15. N

    Symmetric or antisymmetric spontaneous fission

    Is it possible for a nucleus to undergo antisymmetric spontaneous fission? And if so, what is the process responsible? Thanks
  16. Loonuh

    Azimuthally Symmetric Potential for a Spherical Conductor

    Homework Statement Homework Equations /The Attempt at a Solution[/B] I am trying to solve problem 2-13 from my textbook "Principles of Electrodynamics" (see image below). I believe that I should be solving the potential as \varphi(r,\theta) = \sum_{n=0}^\infty (A_n r^n +...
  17. ShayanJ

    Are Green's functions generally symmetric?

    In case of the Green's functions for the Laplace equation, we know that they're all symmetric under the exchange of primed and un-primed variables. But is it generally true for the Green's functions of all differential equations? Thanks
  18. S

    Solution of Schrodinger equation in axially symmetric case

    The following extract is taken from Appendix A of the following paper: http://arxiv.org/abs/0810.0713.Any solution of the Schrodinger equation with rotational invariance around the ##z##-axis can be expanded as ##\psi_{k}=\Sigma_{l}A_{l}P_{l}(cos \theta)R_{kl}(r)##, where ##R_{kl}(r)## are the...
  19. Z

    Normalization condition for free & spherically symmetric

    Homework Statement I think, to normalize a wavefunction, we integrate over the solid angle ##r^2 dr d\theta d\phi##. Typically we have ## R(r)Y(\theta, \phi) ## as solutions. If ##Y## is properly normalized, then the normalization condition for ##R(r)## ought to be $$ \int_0^\infty dr r^2...
  20. S

    Integral with symmetric infinitesimal bounds

    Homework Statement I'm reading something in my quantum physics book that says given a wavefunction ψ that is even, if we evaluate its integral from -ε to ε, the integral is 0. How can this be? I thought this is the property of odd functions. Homework Equations ψ=Aekx if x<0 and ψ=Be-kx if x>0...
  21. M

    Infinite symmetric potential well in one dimension

    1. The problem statement. for Infinite symmetric well -a/2 < x < a/2 in one dimension show that wave function Ψ = Acos(kx) + Bsin(kx) is not physically accepted solution although its mathematically accepted Homework Equations ∫ψ(x)* ψ(x) dx=1
  22. kostoglotov

    Dimension of all 2x2 symmetric matrices?

    I think it's 3... All 2x2 can be written as a_1 A_1 + a_2 A_2 + a_3 A_3 + a_4 A_4 with A_1 = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} , A_2 = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} , A_3 = \begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} , A_4 = \begin{bmatrix} 0 & 0 \\ 0 & 1...
  23. darida

    Electromagnetics in Spherical Symmetric Problem

    In a spherical symmetric problem the only nonzero components of the electric and the magnetic field are Er and Br Why?
  24. Y

    Looking for tighter bound on symmetric PSD matrices products

    Homework Statement Let K and L be symmetric PSD matrices of size N*N, with all entries in [0,1]. Let i be any number in 1...N and K’, L’ be two new symmetric PSD matrices, each with only row i and column i different from K and L. I would like to obtain an upper bound of the equation below...
  25. J

    How to find generators of symmetric groups

    Hi, I was wondering how to find a minimal set of generators for the symmetric groups. Would it be difficult to fill-in the following table? ##\begin{array}{cl} S_3&=\big<(1\;2),(2\;3)\big> \\ S_4&=\big<(1\;2\;3\;4),(1\;2\;4\;3)\big>\\ \vdots\\ S_{500} \end{array} ## Is there a procedure to...
  26. genxium

    Why is stress tensor (in this derivation) symmetric?

    First by "this derivation" I'm referring to an online tutorial: http://farside.ph.utexas.edu/teaching/336L/Fluidhtml/node9.html It's said in the above tutorial that the ##i-th## component of the total torque acting on a fluid element is ##\tau_i = \int_V \epsilon_{ijk} \cdot x_{j} \cdot F_{k}...
  27. Davephaelon

    Symmetric and Antisymmetric Depiction

    I was looking at this excellent website this afternoon, and was puzzled by two diagrams showing the symmetric and antisymmetric wavefunctions. In the latter case the text states that the particles are far away from each other, explaining the Pauli Exclusion Principle, etc. But looking at the...
  28. S

    Product of a symmetric and antisymmetric tensor

    It seems there should be a list of tensor identities on the internet that answers the following, but I can't find one. For tensors in ##R^4##, ##S = S_\mu{}^\nu = S_{(\mu}{}^{\nu)}## is a symmetric tensor. ##A = A_{\nu\rho\sigma}= A_{[\nu\rho\sigma]}## is an antisymmetric tensor in all...
  29. Z

    Heavy Symmetric Top: Obtain Euler Equation Condition

    Hi, I have another problem: Obtain from the Euler equations the condition: These condition for a uniform precession of a heavy symmetric top, imposing that the condition of motion have to be a uniform precession without nutation. I don't know which precisely is the condition to obtain the...
  30. P

    Are heat radiation and absorption symmetric?

    A friend of mine heard a popular science show on the radio. A caller asked what is better to wear on a hot day, white clothes or black clothes. The answer given was that it did not matter because although black absorbs more readily it also radiates it more readily. My friend said of course that...
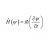
  31. Vitor Pimenta

    Hamiltonian for spherically symmetric potential

    Homework Statement A particle of mass m moves in a "central potential" , V(r), where r denotes the radial displacement of the particle from a fixed origin. From Hamilton´s equations, obtain a "one-dimensional" equation for {\dot p_r}, in the form {{\dot p}_r} = - \frac{\partial }{{\partial...
  32. I

    Proving reflexive, symmetric, transitive properties

    Hello I was reading Spivak's calculus. It starts with discussing the familiar axioms of the real numbers. He calls them properties. At some another forum, I came across the reference to Landau's "Foundation of Analysis" as a background for analysis. So I referred to that book. On the very first...
  33. M

    Expectation value of momentum in symmetric 2D H.O

    Homework Statement Consider the following inital states of the symmetric 2D harmonic oscillator ket (phi 1) = 1/sqrt(2) (ket(0)_x ket(1)_y + ket (1)_x ket (0)_y) ket (phi 2) = 1/sqrt(2) (ket(0)_x ket(0)_y + ket (1)_x ket (0)_y) Calculate the <p_x (t)> for each state Homework EquationsThe...
  34. O

    Equations of Planes from Symmetric Equation of a Line

    Hello,Suppose I have a vector equation: \begin{cases} x=0+10t\\ y=0+10t\\ z=0+10t \end{cases} Which forms the symmetric equation \frac{x-0}{10}=\frac{y-0}{10}=\frac{z-0}{10} Now, I know the symmetric equations can be split up so that you can form the two planes whose intersection yields the...
  35. Avatrin

    Subgroups of Symmetric and Dihedral groups

    I am having problem working with the objects in the title. Working with permutations, rotations and reflections is fine, but I have problem with the following: Showing a subgroup is or is not normal (usually worse in the case of symmetric groups) Finding a subgroup of order n. Showing that...
  36. I

    Determinant and symmetric positive definite matrix

    As a step in a solution to another question our lecture notes claim that the matrix (a,b,c,d are real scalars). \begin{bmatrix} 2a & b(1+d) \\ b(1+d)& 2dc \\ \end{bmatrix} Is positive definite if the determinant is positive. Why? Since the matrix is symmetric it's positive definite if the it...
  37. ShayanJ

    Forming Spherically Symmetric Metric: Math Analysis & Omitted Steps

    In most GR textbooks, the general form of a spherically symmetric metric is obtained by inspection which is acceptable. But in the textbook I'm reading, the author does that with a mathematical analysis just to illustrate the method. But I can't follow his calculations. In fact he omits much of...
  38. PraisetheSun

    Spaghettification inside a spherically symmetric black hole

    I need to find the vectors for time and radius that describe a space-like 4-acceleration of an observer falling radially into a spherically-symmetric black hole. Previous to this question, the values of the real time derivatives for time and radius were derived to be: dt/dτ = (1-2m/r)-1 and...
  39. B

    Derivative of metric with respect to metric

    I'm hoping someone can clarify for me, I have seen the following used: \frac{\partial}{\partial g^{ab}}\left( g^{cd} \right) = \frac{1}{2} \left( \delta_a^c \delta_b^d + \delta_b^c \delta_a^d\right) I understand the two half terms are used to account for the symmetry of the metric tensor...
  40. andres0l1

    W_L-W_R Mixing in the Left-Right Symmetric Model

    Homework Statement The question is how to get the mass term for the W Gauge bosons within the Left Right Symmetric Model (LRSM). My main struggle is with the Left-Right Mixing part. So the LRSM has the gauge group $SU(2)_L\times SU(2)_R \times U(1)_{B-L}$ and with an additional discrete...
  41. R

    Why does this shortcut for eigenvectors of 2x2 symmetric work?

    Hi, I'k looking at some MATLAB code specifically eig2image.m at: http://www.mathworks.com/matlabcentral/fileexchange/24409-hessian-based-frangi-vesselness-filter/content/FrangiFilter2D So, I understand how the computations are done with respect to the eigenvector / eigenvalues and using...
  42. P

    Symmetric and idempotent matrix = Projection matrix

    Homework Statement Consider a symmetric n x n matrix ##A## with ##A^2=A##. Is the linear transformation ##T(\vec{x})=A\vec{x}## necessarily the orthogonal projection onto a subspace of ##R^n##? Homework Equations Symmetric matrix means ##A=A^T## An orthogonal projection matrix is given by...
  43. ognik

    MHB Product of Symmetric and Antisymmetric Matrix

    Hi, I want to show that the Trace of the Product of a symetric Matrix (say A) and an antisymetric (B) Matrix is zero. $So\: (AB)_{ij}=\sum_{k}^{}{a}_{ik}{b}_{kj} $ $and\: Tr(AB)=\sum_{i=j}^{}(AB)_{ij}=\sum_{i}^{}\sum_{k}^{}{a}_{ik}{b}_{ki} $ $because\:A\:is\:symetric, \: {a}_{ik}=...
  44. M

    An example of a relation that is symmetric and anti-symmetric

    Would this example be valid in satisfying a relation that is symmetric and anti-symmetric? The relation R = {(1,1),(2,2)} on the set A = {1,2,3} Also, I'm curious to know since relations can both be neither symmetric and anti-symmetric, would R = {(1,2),(2,1),(2,3)} be an example of such a...
  45. A

    Electromagnetic boundary conditions for symmetric model

    I stumbled upon this article: http://www.comsol.com/blogs/exploiting-symmetry-simplify-magnetic-field-modeling/ Since the article does not contain any mathematical formulations, I was wondering how the boundary conditions can be expressed in terms of magnetic vector potential. From what I...
  46. R

    Symmetric rank-2 tensor, relabelling of indices? (4-vectors)

    Homework Statement Homework Equations Relabelling of indeces, 4-vector notation The Attempt at a Solution The forth line where I've circled one of the components in red, I am unsure why you can simply let ν=μ and μ=v for the second part of the line only then relate it to the first part and...
  47. T

    Proof: τ^2=σ for Odd k-Cycle σ in Symmetric Groups

    If σ is a k-cycle with k odd, prove that there is a cycle τ such that τ^2=σ. I know that every cycle in Sn is the product of disjoint cycles as well as the product of transpositions; however, I'm not sure if using these facts would help me with this proof. Could anyone point me in the right...
  48. K

    MHB Derivatives of symmetric expressions

    So I was bored in math class and came up with this series of related questions, that I cannot answer: Is there a clean expression for $f'(x),$ where $$f(x)=\prod_{i=1}^{n}\dfrac{(x-i)}{(x+i)}?$$ What about for $f''(x)?$ Or for $$f(x)=\prod_{i=1}^{n}\dfrac{(x^2-i)}{(x^2+i)}?$$
  49. binbagsss

    Deriving Max Symmetric Space from Spherically Symmetric - Sean M. Carroll

    I'm looking at Lecture Notes on General Relativity, Sean M. Carroll, deriving the FRW metric, and I'm a little confused with the use of eq 8.4 . I thought instead it should be using the general form of a spherically symmetric metric, not a vacuum spherical symmetric - eq 7.13 has been derived...
  50. P

    Image of a Matrix and symmetric matrix

    Hi, Well I hope it's not a thread that already is in the storage here. I want to understand the image of a matrix. not only calculating it but also why I'm doing that. Here are my questions: 1) They say d = Lx has a solution if d ∈ ImL. I know that the image of a matrix is calculated by Lx = x...
Back
Top