Calculating Tension in a 2 Mass System

[ibriggs]

Homework Statement

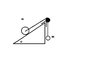
In the ideal setup showin in the following figure, M1=3.0 kg and M2=2.5KG
A) What is the acceleration of the 2 mass system?
B) What is the tension in the string?

Homework Equations

Asys=M2 * g - M1 * g (sin\oslash) / M1 + M2

The Attempt at a Solution

Calculated the acceleration of the system using above equation and obtained:

Asys=1.24 m/s^2

My teacher gave me full credit on that part of my answer. On part B, however, I was expected to find the tension on the string. Here's what I attempted:
Asys=M1(g) -T / M1
1.24 m/s^2 = 2.5(9.8) - T / 5.5 kg

I am thinking I need to also divide by mass 2? Either way, I think I could use a fresh approach at thinking about tension. To me, it just seems like the transferred force through a string...I guess I'm a bit confused.

Thanks in advance,

Ian

 

[rl.bhat]

Asys=M1(g) -T / M1
1.24 m/s^2 = 2.5(9.8) - T / 5.5 kg

1.24 m/s^2 = [2.5(9.8) - T] / 2.5 kg Try this one and find T

 

[ibriggs]

Wow, tell me my mistake wasn't that simple...My new T= -0.127

Thanks guys...I can't even believe I didn't see that!