jerzey101
- 15
- 0
Homework Statement
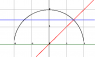
Use polar coordinates to evaluate:
∫sqrt(2)0 ∫sqrt(4-y2)y 1/(1+x2+y2) dxdy
Homework Equations
The Attempt at a Solution
I graphed it and I see r is the part of the elipse sqrt(4-y2) and goes from 0 to ∏/4. I'm not sure how to make the bounds for r or how to covert the function to polar. Does it just convert to 1/(1+r2), then add the conversion factor r?
∫∏/40 ∫?? 1/(1+r2) r drdθ