RED119
- 29
- 3
Homework Statement
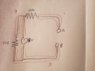
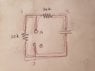
So I need to find the equivalent resistance for the following RC circuit to calculate the time constant, but I got stuck in terms of finding out the equivalent resistance.
Homework Equations
V = IR
The Attempt at a Solution
So the thing I am not sure on is how do you calculate equivalent resistance when there is a capacitor in there? it counts as an element right? so the resistors are in neither series or parallel? or is there a way to calculate the equivalent resistance and I am just missing it? cause the resistors don't share two common but separate nodes with the capacitor in there