Events for frame changing clocks

[ghwellsjr]

Please look at below diagram.

The clocks changes its state from "rest" to "moving" unsimultaneously in S frame, and simultaneously in S' frame.

Now, we look the situation from the perspective of A clock.
Before changing state in S frame, blue events occurs on A clock, and orange events occurs on C clock simultaneously.
After changing state in S frame, red events occurs on A clock, and pink events occurs on C clock simultaneously.
Did you see green events on C clock is skipped for A clock?

Now, we look the situation from the perspective of C clock.
Before changing state in S frame, green events occurs on C clock, and red events occurs on A clock simultaneously.
After changing state in S frame, pink events occurs on C clock, and red events occurs on A clock simultaneously.
Did you see red events on A clock is reoccurred for C clock?

To solve the reoccurring and skipping problem, I have drawn the diagrams in post #20.
Please, read paper provided by DaleSpam in post #15 for detailed information.

Throughout this thread, A, B, and C were just clocks, not observers. Now you want to talk about their perspectives but this is an ambiguous term. Are you asking about what they can actually see and observe or something different?

In post #10, you introduced the idea that what you had previously called red and green events were actually light pulses. And now you have more different colored light pulses so are you now asking about what A sees of C's different colored light pulses and what C sees of A's different colored light pulses? There is only one answer to this question.

Or are you asking something different? If it is something different, then you need to specify exactly what that something different is because there are an infinite number of different questions with an infinite number of different answers and I have no way of knowing what you have in mind.

 

[Mentz114]

I couldn't understood the term "casual contact" before. And I still can't understand the term. What is meaning of "casual contact" or "directly observable"?

Two events along two worldlines are not causally connected if the proper interval between them is spacelike. This means that one of them is outside the others past light cone. In the 'now' of either event the other event will not be observable until 'now + later' of the observing WL.

 

[mananvpanchal]

Throughout this thread, A, B, and C were just clocks, not observers. Now you want to talk about their perspectives but this is an ambiguous term. Are you asking about what they can actually see and observe or something different?

In post #10, you introduced the idea that what you had previously called red and green events were actually light pulses. And now you have more different colored light pulses so are you now asking about what A sees of C's different colored light pulses and what C sees of A's different colored light pulses? There is only one answer to this question.

Or are you asking something different? If it is something different, then you need to specify exactly what that something different is because there are an infinite number of different questions with an infinite number of different answers and I have no way of knowing what you have in mind.

This is the confusion: I am not asking you. I just telling you.
I am just trying to explain you the problem which is solved. But, I cannot understand why you are not understanding.

 

[mananvpanchal]

Two events along two worldlines are not causally connected if the proper interval between them is spacelike. This means that one of them is outside the others past light cone. In the 'now' of either event the other event will not be observable until 'now + later' of the observing WL.

Thanks Mentz114.

 

[ghwellsjr]

Throughout this thread, A, B, and C were just clocks, not observers. Now you want to talk about their perspectives but this is an ambiguous term. Are you asking about what they can actually see and observe or something different?

In post #10, you introduced the idea that what you had previously called red and green events were actually light pulses. And now you have more different colored light pulses so are you now asking about what A sees of C's different colored light pulses and what C sees of A's different colored light pulses? There is only one answer to this question.

Or are you asking something different? If it is something different, then you need to specify exactly what that something different is because there are an infinite number of different questions with an infinite number of different answers and I have no way of knowing what you have in mind.

This is the confusion: I am not asking you. I just telling you.
I am just trying to explain you the problem which is solved. But, I cannot understand why you are not understanding.

You're right, you weren't asking. You said you wanted me to look at the situation from the perspective of clock A and then from the perspective of clock C. But I don't know what you mean by "perspective". Do you mean what A and C can actually see or do you mean something different?

 

[mananvpanchal]

You're right, you weren't asking. You said you wanted me to look at the situation from the perspective of clock A and then from the perspective of clock C. But I don't know what you mean by "perspective". Do you mean what A and C can actually see or do you mean something different?

Please, don't get tensed too much. I know that clocks cannot observe. But, this is simple way to tell something. Let's think about three observes holding that clocks. Now, is this fine?

 

[ghwellsjr]

You're right, you weren't asking. You said you wanted me to look at the situation from the perspective of clock A and then from the perspective of clock C. But I don't know what you mean by "perspective". Do you mean what A and C can actually see or do you mean something different?

Please, don't get tensed too much. I know that clocks cannot observe. But, this is simple way to tell something. Let's think about three observes holding that clocks. Now, is this fine?

That's fine.

Now when you say you want me to look at the situation from the perspectives of each of the observers holding the different clocks, do you mean what the observers can actually see or do you mean something different?

 

[mananvpanchal]

That's fine.

Now when you say you want me to look at the situation from the perspectives of each of the observers holding the different clocks, do you mean what the observers can actually see or do you mean something different?

No, I don't mean what observer see. When we are talking about some simultaneous events we don't worry about when the events will be observed. I am just telling that some events is simultaneous for some observer. that's it.

The blue and orange events are simultaneous for A observer.
The red and pink events are simultaneous for A observer.
The green and red events are simultaneous for C observer.
The pink and red events are simultaneous for C observer.

 

[ghwellsjr]

No, I don't mean what observer see. When we are talking about some simultaneous events we don't worry about when the events will be observed. I am just telling that some events is simultaneous for some observer. that's it.

The blue and orange events are simultaneous for A observer.
The red and pink events are simultaneous for A observer.
The green and red events are simultaneous for C observer.
The pink and red events are simultaneous for C observer.

What you are doing is implicitly selecting the frame in which the observer is at rest. This can work unambiguously for three of the four cases you presented above because both the observer and the remote clock are at rest in the same frame and therefore we can talk about light pulse events being simultaneous. But it doesn't work unambiguously for the third case because C observer is not at rest with respect to A clock during the time interval of the green events. If you say that the pink and red events are simultaneous in S frame, then, of course they are simultaneous for C observer in his implied rest S frame but now you are forcing the red and green light pulses to occur at different time intervals in their own rest frames without any way to co-ordinate the timing intervals of the two sets of clocks.

You stated in post #3 that you wanted the clocks to emit light pulses at regular intervals of time and your drawing in post #31 appears to show that. The problem is that as soon as A clock changes speed and before C observer and C clock change their speed, there can not be any more simultaneous light pulse events between clock A and observer C with his clock C because the clocks are ticking at different rates. And the only way that we can say that the light pulse events after C observer/clock change their speed are simultaneous is if they happen to be simultaneous with A clock and we ignore the fact that the times on the clocks are no longer ticking synchronously in their common rest frame.

But you said earlier that you weren't concerned about these issues, you were only concerned about the simultaneity of events. Please go back and look at yuiop's post #7 where he illustrated these issues perfectly and your discount of his post in your post #10.

You can't have it both ways, you either care about the timing on the clocks which cause the light pulse events to be simultaneous or you don't care about the timing on the clocks and simply define arbitrary events to be simultaneous in the two frames.

One more thing: you set up your scenario in such a way that the three clocks started out at rest in the S frame and then you stated that they change speed simultaneously in the S' frame to become at rest in the S' frame. How did each clock know when to fire its rocket (or whatever) to cause this simultaneous change in speed in the S' frame?

 

[mananvpanchal]

What you are doing is implicitly selecting the frame in which the observer is at rest. This can work unambiguously for three of the four cases you presented above because both the observer and the remote clock are at rest in the same frame and therefore we can talk about light pulse events being simultaneous. But it doesn't work unambiguously for the third case because C observer is not at rest with respect to A clock during the time interval of the green events. If you say that the pink and red events are simultaneous in S frame, then, of course they are simultaneous for C observer in his implied rest S frame but now you are forcing the red and green light pulses to occur at different time intervals in their own rest frames without any way to co-ordinate the timing intervals of the two sets of clocks.

You stated in post #3 that you wanted the clocks to emit light pulses at regular intervals of time and your drawing in post #31 appears to show that. The problem is that as soon as A clock changes speed and before C observer and C clock change their speed, there can not be any more simultaneous light pulse events between clock A and observer C with his clock C because the clocks are ticking at different rates. And the only way that we can say that the light pulse events after C observer/clock change their speed are simultaneous is if they happen to be simultaneous with A clock and we ignore the fact that the times on the clocks are no longer ticking synchronously in their common rest frame.

The red and pink events is occurred simultaneously in S' frame not in S frame.

Yes, I have stated that the events is occurred at some unit time interval. But, that was over requirement to explain the problem. To explain the problem I actually don't need events occurred at some unit time interval, I don't need readings of clocks, I don't need to bother about synchronization of the clocks.

But you said earlier that you weren't concerned about these issues, you were only concerned about the simultaneity of events. Please go back and look at yuiop's post #7 where he illustrated these issues perfectly and your discount of his post in your post #10.

You can't have it both ways, you either care about the timing on the clocks which cause the light pulse events to be simultaneous or you don't care about the timing on the clocks and simply define arbitrary events to be simultaneous in the two frames.

As I said before events has nothing to do with timings of clocks.

One more thing: you set up your scenario in such a way that the three clocks started out at rest in the S frame and then you stated that they change speed simultaneously in the S' frame to become at rest in the S' frame. How did each clock know when to fire its rocket (or whatever) to cause this simultaneous change in speed in the S' frame?

Clocks don't know, I know that when to fire its rocket. I have showed this in diagram that when I have fired its rocket.

See, I had a problem which is solved. But, I cannot understand what is your problem.
Do you not agree with problem?
or
Do you not agree with solution?

 

[ghwellsjr]

You presented a scenario in your first post that you believed had a problem that you did not know how to solve using the normal methods of Special Relativity. People do this all the time on this forum. They usually call these problems paradoxes because when viewed by two different Frames of Reference, they believe there is an inconsistency or a conflict in Special Relativity.

The reason why these people believe there is a problem is because they don't understand Special Relativity and so we try to help them learn Special Relativity until they can understand why the problem they presented is not a problem. Sometimes our explanations help but other times, despite our best efforts, these people continue to struggle with the concepts of Special Relativity and never arrive at the point where they realize there was no problem.

You are different from most people. In spite of the fact that you continue to believe that your scenario presents a problem that cannot be handled by the normal methods of Special Relativity, you believe that there is an extraordinary solution that does solve the problem that you presented. Whether or not that solution actually works is immaterial if you continue to believe that it is the only way to solve the problem you presented. That's what concerns me.

You have made a lot of statements in this thread that indicate to me that you do not understand the basics of Special Relativity. Here's one from post #5:

I have defined some events in diagram (red events and green events). A can define red events in its S' frame and C can define the same events in its S frame. Same for green events, A can define green events in its S' frame and C can define the same events in its S frame. The all events is defined by two co-ordinate system for A and C.

I explained what was wrong with your idea in post #12:

2) When you define or specify an event in one inertial co-ordinate system, you have already defined and specified it for all other inertial co-ordinate systems and you must use the Lorentz Transformation as the means to obtain the co-ordinates in those other systems. It always produces a time component, as well as three spatial co-ordinates in any other system you want. There are no exceptions.

And you said that was fine but then you continued to express the same problem. What you don't seem to realize is that you can formulate, analyze, demonstrate, present and understand any scenario in Special Relativity (which excludes scenarios involving gravity) using any single inertial Frame of Reference, you don't need two co-ordinate systems for A and C as you stated and as you continue to state.

Your perceived problem is that A, B, and C change frames when they change speeds and since they each do it at different times, this leads you to believe during the transition, there are some events which "disappear" for C and are "duplicated" or "repeated" for A and this is a problem that you believe cannot be handled by the normal single-frame approach but can only be handled by using a very complicated non-linear definition of a frame.

I'm not saying that the complicated non-linear definition of a frame is wrong or that it doesn't also provide an alternate "solution" to your "problem", I'm just saying that it is unnecessary to "solve" your "problem" in that very complicated way and that it is wrong and a misunderstanding of Special Relativity to believe that it is the "only" way or even a "better" way than the normal linear single-frame approach.

It would be one thing if you presented evidence and understanding that your scenario could be explained by any single linear Frame of Reference such as the one you called S or the one you called S' or any other linear frame but you haven't provided any. You have consistently indicated that these won't work but rather it takes two frames, S for the first part and S' for the second part and then you see a problem with that particular two-frame approach. Yes, that is a problem for you to believe that you need two frames but the solution is not to insist on a single non-linear frame but rather to understand that either the S frame all by itself will work with no problem or the S' frame all by itself will also work with no problem or any other single linear frame, they are all equally valid and none is preferred, certainly not a non-linear frame.

 

[yuiop]

The red and pink events is occurred simultaneously in S' frame not in S frame.

Yes, I have stated that the events is occurred at some unit time interval. But, that was over requirement to explain the problem. To explain the problem I actually don't need events occurred at some unit time interval, I don't need readings of clocks, I don't need to bother about synchronization of the clocks.

I find it odd that you think you don't need to bother with synchronisation of the clocks when considering whether events occurred simultaneously or not. You seem to think that simultaneity is a natural phenomena and you liked the explanation that the new line of simultaneity spreads out at the speed of light. However, you do not seem to be aware that simultaneity for spatially separated objects is just a convention that is determined by the method you use to synchronise the clocks. You cannot separate simultaneity from synchronisation of clocks. When we use the Einstein synchronisation method we assume that the one way speed of light is isotropic in all directions, but that is just an assumption and the one way speed of light has never been measured and cannot be measured even in principle. It is inherently unknowable. If we do not assume the speed of light is equal in different directions, then the LoS is not necessarily horizontal in frame S in the first place. I demonstrated in a diagram in #7 that when the clocks accelerate to a new rest frame S' they are no longer (Einstein) synchronised in frame S or S'. They are however still synchronised if we use a synchronisation convention that does not assume that the one way speed of light is the same in all directions. The change in LoS spreading out at the speed of light is just an artificial construct and is just a representation of how fast we can artificially re-sychronise the clocks because that is how long it takes to realize a change has occurred. It is especially artificial when we accelerate more than one spatially separated clock (as in your scenario) because we arbitrarily have to select one master clock

To show how artificial it is, consider some clocks on the rim of a large disc. Let us say the disc is initially not rotating and we sychronise the clocks using the Einstein synchronisation method that assumes isotopic one way speed of light. Now we spin the disc clockwise to relativistic speeds without adjusting any clocks. Observers on the disc would now measure the one way speed of light to be different in different directions. If they now try and resychronise the clocks using the Einstein convention, they find it impossible to do all the way around the disc and they end up with something similar to the international date line where there is a discontinuous jump in time at some arbitrary location on the rim of the disc. Even if they do use this artificial method of resynchronisation, they will find that if they use mirrors to measure the speed of light all the way around the disc that it takes more time to go all the way around the disc clockwise than it takes to go in the other direction when they use any single clock and they cannot get away from the isotropic speed of light in an accelerating reference frame, no matter what convention they use.

 

[mananvpanchal]

Hello ghwellsjr,

You says that we can observe the scenario from any frame, and we get solution. But, here we are not talking about two inertial frame. Here is a non-inertial frame which is made by two sub part of two inertial frame.

http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_vase.html

Please, see figure 4 in above link. In this case there are one inertial frame in which terence is at rest and one non-inertial frame in which stella is at rest.

The time gap is created in terence's frame for stella. Stella misses all the events of terence's world line which is lies in the time gap. We know that this is the cause of age difference between stella and terence. Actually the time gap helps us in solving the paradox. But, if we look closely the time gap is a big problem in its own. So, to remove the skipping events problem we have to take help from the new method for defining LoS.

 

[ghwellsjr]

Hello ghwellsjr,

You says that we can observe the scenario from any frame, and we get solution.

I'm not the only one saying that, I'm just repeating what Einstein said and what your paper says near the top:

Relativity ... says to us, "Pick whichever frame you like to describe your results. They're all equivalent."

Do you disagree?

But, here we are not talking about two inertial frame. Here is a non-inertial frame which is made by two sub part of two inertial frame.

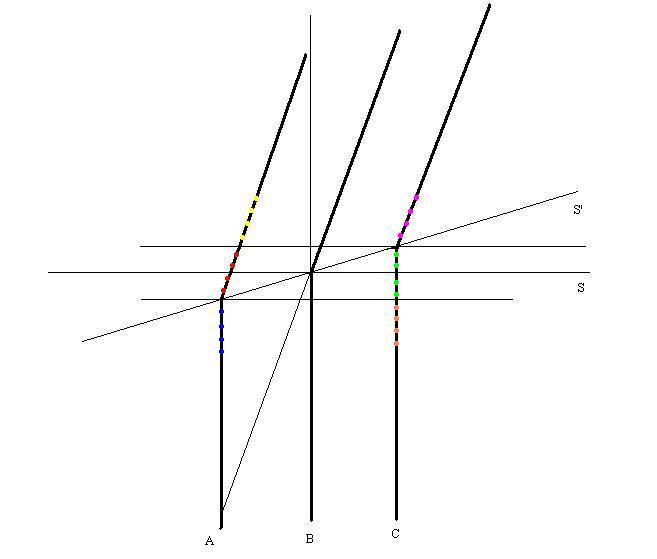
http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_vase.html

Please, see figure 4 in above link. In this case there are one inertial frame in which terence is at rest and one non-inertial frame in which stella is at rest.

In a frame in which terence is at rest, stella is moving during the entire scenario. You can analyze everything about both terence and stella from this one frame. Do you disagree?

There is another inertial frame in which stella is at rest during the outbound leg of her trip and moving during the inbound leg of her trip and in which terence is moving during the entire scenario. You can analyze everything about both terence and stella from this one frame. Do you disagree?

There is another inertial frame in which stella is moving during the outbound leg of her trip and at rest during the inbound leg of her trip and in which terence is moving during the entire scenario. You can analyze everything about both terence and stella from this one frame. Do you disagree?

There are an infinite number of additional inertial frames in which both terence and stella are both moving for the entire scenario. You can analyze everything about both terence and stella from any of these inertial frames. Do you disagree?

All of these frames employ the same well-defined method of description and analysis, and they all produce the same result in terms of the final age difference between terence and stella. None of these frames are preferred over any of the others and none of them have any "problem" with regard to missing or duplicated events. Do you disagree?

There are an infinite number of additional non-inertial frames in which you can contort the analysis just about any way you choose. There is no well-defined method of how to do this. Every example is unique. Some may introduce missing events or duplicated events but if they are done correctly, they will still also produce the same result in terms of the final age difference between terence and stella. None of these non-inertial frames are preferred over any of the other non-inertial frames or inertial frames. Do you disagree?

The time gap is created in terence's frame for stella.

That's not what the article says. It says the gap is in terence's world line, not in his reference frame.

Stella misses all the events of terence's world line which is lies in the time gap.

That's not what the article says. It says the gap is devoid of blue lines, meaning it's devoid of events.

We know that this is the cause of age difference between stella and terence.

No it isn't the cause of the age difference. The age difference can be analyzed from any inertial frame in which there are no gaps, no missing events, no duplicated events, no non-linearities, no non-inertial frames, no convoluted random stitching of other disjointed sub-frames, etc. Just simple application of Special Relativity. Clocks moving in any inertial frame tick at a slower rate the faster they move. Therefore, a moving clock will accumulate less time than a stationary clock. Real simple. But as your article pointed out, "there are some pitfalls for the unwary" and I think the author fell into one of the pits when he said below Figure 3, "From the viewpoint of Stella, her clock is running much faster than Terence's during the turnaround." Seems to me that it's the other way around.

Actually the time gap helps us in solving the paradox.

No it doesn't, it just creates a new problem.

But, if we look closely the time gap is a big problem in its own.

You're right about that.

So, to remove the skipping events problem we have to take help from the new method for defining LoS.

If you had only stuck with a single inertial frame, you wouldn't have any skipping events problem that needed to be solved.

Please understand, I'm not saying that any of the analyses in the article are wrong, not even the one that you see a problem with, or that the "new method for defining LoS" is wrong, they just are unnecessary. You misunderstand Special Relativity if you think that a single inertial frame is inadequate to solve any problem (devoid of gravity) or that any non-inertial frame is better at solving any problem (devoid of gravity).

After you answer all my questions in bold, I would like you to explain to me the "new method for defining LoS", please.

 

[mananvpanchal]

Ok, if any single inertial frame can explain everything then pick up S and/or S' and please explain me my original post. The requirement is there should not be any duplicating and skipping events.

 

[Dale]

Ok, if any single inertial frame can explain everything then pick up S and/or S' and please explain me my original post. The requirement is there should not be any duplicating and skipping events.

In S first A accelerates then B accelerates then C accelerates. Each red and the cooresponding green dots are simultaneous in S.

No events are duplicated nor skipped.

 

[Mentz114]

The requirement is there should not be any duplicating and skipping events.

Obviously, if we send two light beams, one in each direction, from any point on any of the worldlines, then every other WL will receive news of the event in some (finite) time, and once only. So no event can possibly be missed or duplicated by realistic observers on those WLs.

I believe the duplicating and skipping events is due to an incorrect use of the LT, ignoring signal spped and making incorrect assumptions about events lying on LoS, which are naturally not causally connected.

Incorporating the finite signal speed, for instance by using the times and locations assigned by a radar-observer ( Dolby & Gull's method) any hint of this weirdness disappears. Causality rules.

After you answer all my questions in bold, I would like you to explain to me the "new method for defining LoS", please.

This refers to the Dolby&Gull paper, the link is in a Dalespam post earlier http://arxiv.org/abs/gr-qc/0104077

 

[ghwellsjr]

Ok, if any single inertial frame can explain everything then pick up S and/or S' and please explain me my original post. The requirement is there should not be any duplicating and skipping events.

Did you read post #44 where I said that yuiop already provided this for you and you rejected it? Look at post #7 where he drew it from the point of view of the S frame. Do you want something more?

 

[yuiop]

Ok, if any single inertial frame can explain everything then pick up S and/or S' and please explain me my original post. The requirement is there should not be any duplicating and skipping events.

If it helps, sketch the paths in your OP diagram on the first applet on this web page:

http://www.reagenix.com/personal/sci/space_time/test.html

Now label some events using the right mouse button and then move the slider at the top left or right. Moving the slider is the same as changing to a new reference frame. Notice that in any reference frame, none of the labelled events get skipped or duplicated. Does that answer your question?

 

[ghwellsjr]

Ok, if any single inertial frame can explain everything then pick up S and/or S' and please explain me my original post. The requirement is there should not be any duplicating and skipping events.

OK. I have taken the diagram from your original post and put co-ordinates on it that seemed reasonable to me. I'm assuming that c=1 so the vertical axis is time in seconds and the horizontal axis is the x-position in light-seconds. The co-ordinates are shown as [t,x]. I show the co-ordinates for the three events where each clock changes speed and for each of the four red events and each of the four green events.

All these co-ordinates are for the S frame:

Notice that the green and red events are paired in that each pair is simultaneous in the S frame as depicted by the three horizontal lines. (I could have drawn four more lines going through each pair of simultaneous events but I didn't do it since you didn't do it.)

Now, the exact same diagram but with all the co-ordinates transformed to the S' frame which I am assuming is moving at a speed of 0.4c with respect to the S frame:

Now you can see that the red and green pairs are not simultaneous in the S' frame but the three speed-changing events are since they all occur at time zero. Also note that the four red events are at the same location in the S' frame, meaning that they occur at different times but at the same location in the S' frame.

But notice that the co-ordinates are not aligned with the axes so I have redrawn the diagram so that the S' frame is aligned and the S frame is skewed but otherwise, this is exactly the same information that is contained in the previous image:

Now it is really obvious that the three speed changing events are simultaneous since in addition to their time co-ordinates all being zero, the events are on the same horizontal line.

It is also obvious that the four red events all occur at the same location in the S' frame since they are on a vertical line (and their position co-ordinates are the same) and that the four green events are not at the same location.

Finally, it is obvious that the pairs of green-red events that were simultaneous in the S frame are not simultaneous in the S' frame since they are not on a horizontal line of simultaneity. The LoS from the S frame are now shown skewed.

Notice that no events have disappeared or are duplicated in any of the diagrams.

 

[mananvpanchal]

If it helps, sketch the paths in your OP diagram on the first applet on this web page:

Thanks, I have been trying to find something like this from long.

 

[mananvpanchal]

George

Great work. I appreciate it. But, I know that we can define all the events in any co-ordinate system.

By the way, third diagram doesn't show contracted length between clocks.

First two diagram shows proper length in S frame at same time is greater than contracted length in S frame at same time.
Please, see the distance between A and C clocks at first LoS of S frame and at second LoS of S. The distance at first LoS is shorter than the distance at second LoS.

But, in third diagram proper length in S' frame at same time is equal to contracted length in S' frame at same time.
Please, draw two horizontal LoS of S' frame, one above spatial axis and other below spatial axis. You would see that both distance is same at both LoS of S' frame.

 

[ghwellsjr]

George

Great work. I appreciate it. But, I know that we can define all the events in any co-ordinate system.

Then why did you start this thread?

By the way, third diagram doesn't show contracted length between clocks.

That's because I just inverted your drawing instead of re-drawing it from scratch. Just go by the values of the co-ordinates and assume the diagram is to a different scale. The point of the drawing is only to show that no events disappear and no events are duplicated, a point which you now claim you knew all along.

First two diagram shows proper length in S frame at same time is greater than contracted length in S frame at same time.
Please, see the distance between A and C clocks at first LoS of S frame and at second LoS of S. The distance at first LoS is shorter than the distance at second LoS.

Yes, because in the S frame, the A clock starts moving toward the C clock before the C clock starts its motion so the distance between the A and C clocks gets smaller. It goes from 200 light-seconds to 168 light-seconds. (I didn't show the event that would make this clear, because you didn't show that event either and I didn't think this exercise was about proper lengths, only about lines of simultaneity and about the disappearance or duplication of events in different frames.)

But, in third diagram proper length in S' frame at same time is equal to contracted length in S' frame at same time.
Please, draw two horizontal LoS of S' frame, one above spatial axis and other below spatial axis. You would see that both distance is same at both LoS of S' frame.

Yes, because in the S' frame, the clocks all change their speeds simultaneously and so their distance apart remains a constant 183.3 light-seconds, both before and after the change in speed.

But why are you now pointing out the differences in proper lengths according to different frames when the whole point of this thread had to do with duplicated or disappearing events?