afromanam
- 16
- 0
Thanks for the help,
i think I'm getting it, but i still have doubts, anyway, here's the problem:
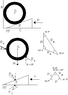
A wedge of 15° is pushed under a tube of 50 kg as shown in fig 1. \mu_S = 0.20 in all the surfaces. Determine the required force P to move the wedge.
answer is P &= 283 N\leftarrow
but i get 377.73 N, please give some hints of what I'm doing wrong
what I'm doing is (please refer to attachments to see the fbd's)
\arctan\mu_S = \theta_S
\arctan0.20 = \theta_S
11.3 &= \theta_S
R &_B=\frac{W\sin101.3}{\sin52.4}
R &_B=607.09 N
and in the second system:
P &=\frac{607.09N\sin37.6}{sin78.7}
which yields:
P &=377.3N\leftarrow
please help!
thanks in advance for any help you can give me
i think I'm getting it, but i still have doubts, anyway, here's the problem:
A wedge of 15° is pushed under a tube of 50 kg as shown in fig 1. \mu_S = 0.20 in all the surfaces. Determine the required force P to move the wedge.
answer is P &= 283 N\leftarrow
but i get 377.73 N, please give some hints of what I'm doing wrong
what I'm doing is (please refer to attachments to see the fbd's)
\arctan\mu_S = \theta_S
\arctan0.20 = \theta_S
11.3 &= \theta_S
R &_B=\frac{W\sin101.3}{\sin52.4}
R &_B=607.09 N
and in the second system:
P &=\frac{607.09N\sin37.6}{sin78.7}
which yields:
P &=377.3N\leftarrow
please help!
thanks in advance for any help you can give me
Attachments
Last edited: