- #1
Ceva
- 12
- 1
Hello, there is a not-hard-at-all problem i am struggling with and i am must be missing something.
1. Homework Statement
An end of a light wire rod is bent into a hoop of radius r. The straight part of the rod has length l; a ball of mass M is attached to the other end of the rod. The pendulum thus formed is hung by the hoop onto a revolving shaft. The coef- ficient of friction between the shaft and the hoop is µ. Find the equilibrium angle between the rod and the vertical.
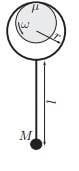
I am going to work with the torque of forces. I am taking the torques about O, where the shaft and the hoop are in contact, so that the torque of friction is zero. Also, the torque of the tension of wire S is zero as it passes through O.
The condition where slipping begins on an inclined plane is tanθ = μ. (where θ here is i guess the angle between the horizontal plane and Friction).
My diagram:
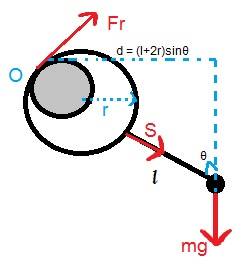
If i am to work only with the torque of mg, how can i reach a solution for μ? The torque equation just gives me:
μmg(l+2r)cosθ=0.
1. Homework Statement
An end of a light wire rod is bent into a hoop of radius r. The straight part of the rod has length l; a ball of mass M is attached to the other end of the rod. The pendulum thus formed is hung by the hoop onto a revolving shaft. The coef- ficient of friction between the shaft and the hoop is µ. Find the equilibrium angle between the rod and the vertical.
Homework Equations
The Attempt at a Solution
I am going to work with the torque of forces. I am taking the torques about O, where the shaft and the hoop are in contact, so that the torque of friction is zero. Also, the torque of the tension of wire S is zero as it passes through O.
The condition where slipping begins on an inclined plane is tanθ = μ. (where θ here is i guess the angle between the horizontal plane and Friction).
My diagram:
If i am to work only with the torque of mg, how can i reach a solution for μ? The torque equation just gives me:
μmg(l+2r)cosθ=0.
Last edited: