ineedhelp1234
- 6
- 0
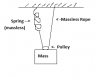
A massless spring of constant k=196 N/m is used to suspend the mass M=1.45 kg (including the pulley), as shown in the attached figure. What is the frequency of simple harmonic motion?
Relevant equations
f = 1/period
T = 2pi*sqrt(M/k)
Tension = 1/2Mg
What I tried...
T(tension on spring) = 1/2Mg <-- since each rope has equal tension?? with that, I found that the mass acting on the spring would be M/2 since the tension is half of the weight?? I feel like this may be where I'm going wrong..
f = 1/(period) = (1/2pi)*sqrt(k/m)
f = 2.62 /hz
I know I'm doing something wrong, I'm just not sure how what I need to change. Any explanations would be great!
Relevant equations
f = 1/period
T = 2pi*sqrt(M/k)
Tension = 1/2Mg
What I tried...
T(tension on spring) = 1/2Mg <-- since each rope has equal tension?? with that, I found that the mass acting on the spring would be M/2 since the tension is half of the weight?? I feel like this may be where I'm going wrong..
f = 1/(period) = (1/2pi)*sqrt(k/m)
f = 2.62 /hz
I know I'm doing something wrong, I'm just not sure how what I need to change. Any explanations would be great!